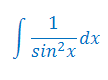Podaj wzór na całkę nieoznaczoną
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Kategorie zadań z rozwiązaniami z matematyki wyższej
- Całki nieoznaczone (121)
- Całki oznaczone (32)
- Całki niewłaściwe (24)
- Całki podwójne (16)
- Całki potrójne (8)
- Całki krzywoliniowe (14)
Całki - zadania z rozwiązaniami
Podaj wzór na całkę nieoznaczoną
Podaj wzór na całkę nieoznaczoną
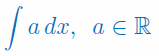
Podaj wzór na całkę nieoznaczoną
Podaj wzór na całkę nieoznaczoną
Oblicz całkę nieoznaczoną
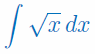
Oblicz całkę nieoznaczoną
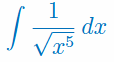
Oblicz całkę nieoznaczoną
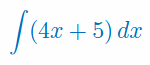
Oblicz całkę nieoznaczoną
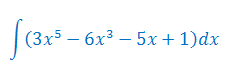
Podaj wzór na całkę nieoznaczoną
Podaj wzór na całkę nieoznaczoną
Oblicz całkę nieoznaczoną
Oblicz całkę nieoznaczoną
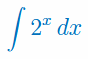
Oblicz całkę nieoznaczoną
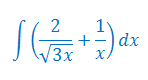
Oblicz całkę nieoznaczoną
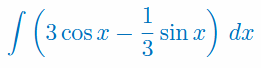
Oblicz całkę nieoznaczoną
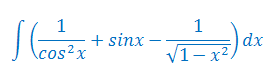
Oblicz całkę nieoznaczoną
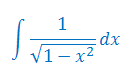
Podaj wzór na całkę nieoznaczoną z funkcji \(\frac{1}{\sin^2x}\)
Podaj wzór na całkę nieoznaczoną z \(\frac{1}{\cos^2x}\)
Podaj wzór na całkę nieoznaczoną
Podaj wzór na całkę nieoznaczoną
Oblicz całkę nieoznaczoną
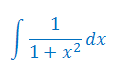
Oblicz całkę nieoznaczoną
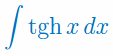
Oblicz całkę nieoznaczoną
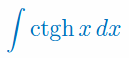
Oblicz całkę nieoznaczoną
Oblicz całkę nieoznaczoną
Oblicz całkę nieoznaczoną
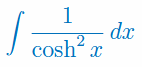
Oblicz całkę nieoznaczoną
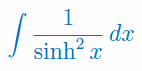
Wyprowadź wzór na całkowanie przez podstawienie
\[{\int f(g(x))g'(x)\, dx=\int f(t)dt=F(g(x))+c}\quad\quad\quad\]
gdzie \(F(x)\) jest funkcją pierwotną funkcji \(f(x)\).
Wyprowadź wzór na całkowanie przez części
\[{\int f'(x)g(x)\,dx=f(x)g(x)-\int f(x)g'(x)\,dx}\quad\quad\quad\,\,\]
Wyprowadź wzór stosując całkowanie przez podstawienie
\[{\int \frac{f'(x)}{f(x)}\, dx=\ln|f(x)|+c}\quad\quad\quad\quad\,\,\]
Oblicz całkę nieoznaczoną

Oblicz całkę nieoznaczoną

Oblicz całkę nieoznaczoną

Oblicz całkę nieoznaczoną

Oblicz całkę nieoznaczoną

Oblicz całkę nieoznaczoną

OBlicz całkę nieoznaczoną

OBlicz całkę nieoznaczoną

Oblicz całkę nieoznaczoną

Oblicz całkę nieoznaczoną
Oblicz całkę nieoznaczoną
Oblicz całkę nieoznaczoną
Oblicz całkę nieoznaczoną

Oblicz całkę nieoznaczoną
Oblicz całkę nieoznaczoną

Oblicz całkę nieoznaczoną
Oblicz całkę nieoznaczoną

Oblicz całkę nieoznaczoną

Oblicz całkę nieoznaczoną

Jesteś w kategorii Całki zadania z rozwiązaniami
W tym dziale do Twojej dyspozycji jest kilkaset przykładów i zadań z pełnymi rozwiązaniami z zakresu całek, w tym całek nieoznaczonych, oznaczonych, niewłaściwych, podwójnych, potrójnych i krzywoliniowych. Działy tematyczne obejmują najprostsze zagadnienia, takie jak całki funkcji elementarnych (funkcji trygonometrycznych, potęgowych, eksponencjalnych, logarytmicznych itd.) oraz trudniejsze tematy takie jak całkowanie przez części i przez podstawienie. Zadania w każdym dziale często uporządkowane są pod względem rosnącego poziomu trudności.
Niestety, nauka liczenia całek (całkowania funkcji), jak zresztą również innych działów matematyki, jest jak domino, musisz dobrze opanować podstawowe zagadnienia, żeby móc opanować trudniejszy materiał, z całkami jest dokładnie tak samo. Całkowanie to operacja odwrotna do różniczkowania, czyli liczenia pochodnej. Zatem, aby nauczyć się całkować funkcjie musisz umieć liczyć pochodne. Jeśli jeszcze nie umiesz różniczkować funkcji, to zachęcam do zapoznania się z działem "Podstawy" a następnie z działem "Pochodna funkcji".
Warto próbować samodzielnie rozwiązać jak największą liczbę zadań z całek i sięgać do rozwiązań zamieszczonych na stronie jedynie w ramach podpowiedzi lub w celu sprawdzenia wyniku. Pod każdym zadaniem jest możliwość zadania pytania w komentarzu, warto z tej opcji korzystać, ponieważ tylko zrozumienie rozwiązania zadania (oraz schematów i pojęć, które zostały użyte) w 100% pozwala później na samodzielne rozwiązanie podobnego zadania w czasie trwania kolokwium, czy egzaminu. Zachęcam do konsekwentnej nauki całek na przykładach, która przynosi zdecydowanie najlepsze efekty (potwierdzone naukowo). Powodzenia w nauce całek!