Start 
Znajdź wszystkie liczby zespolone \(z\) spełniające równanie:
\(\frac{z+1}{\overline{z}-1}=-1\)
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Równania zespolone - zadania z rozwiązaniami
Znajdź wszystkie liczby zespolone \(z\) spełniające równanie:
\(z=\overline{z}\)
Znajdź wszystkie liczby zespolone \(z\) spełniające równanie:
\(z=|z|\)
Znajdź wszystkie liczby zespolone \(z\) spełniające równanie:
\(z\cdot (1+i)=1\)
Znajdź wszystkie liczby zespolone \(z\) spełniające równanie:
\({z=2+3i-2z}\)
Znajdź wszystkie liczby zespolone \(z\) spełniające równanie:
\({z^2=i}\)
Rozwiąż równanie zespolone:
Rozwiąż równanie zespolone:
Rozwiąż równanie zespolone:
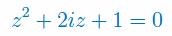
Znajdź wszystkie liczby zespolone z spełniające podane równanie:
Rozwiąż równanie zespolone:
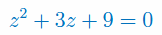
Rozwiąż równanie zespolone:
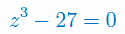
Rozwiąż równanie zespolone:
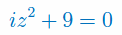
Rozwiąż równanie zespolone:
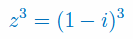
Rozwiąż równanie zespolone:
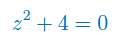
Rozwiąż równanie zespolone wiedząc, że \(Im(z)=1\):
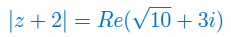
Rozwiąż równanie zespolone:
Rozwiąż równanie zespolone:
Rozwiąż równanie zespolone:
Rozwiąż równanie zespolone porównując części rzeczywiste i urojone obu stron równania:
Rozwiąż równanie zespolone:
Znajdź wszystkie liczby zespolone spełniające równanie:
\((z+1)^n-(z-1)^n=0\)
gdzie \(n\in\mathbb{N}\).
Znajdź wszystkie wartości rzeczywiste parametru t, dla których spełnione są warunki
\(z^2=t+8i,\,\,\,\,\,\,\arg(z^2)=\frac{3}{4}\pi\)
Rozwiąż równanie zespolone:
\(z^4=1\)
Rozwiąż równanie zespolone:
\(z^3=1\)
Rozwiąż równanie zespolone:
\(z^3=\overline{z}\)
Rozwiąż równanie zespolone:
\(z^2=\overline{z}\)
Rozwiąż równanie zespolone:
\(1^x=-1\)
Jesteś w kategorii Równania zespolone zadania z rozwiązaniami
Istnieje wiele typów równań zespolonych od łatwych do rozwiązania równań, w których mamy tylko liczby zespolone w postaci elgebraicznej, po takie w których występują sprzężenia, część rzeczywista i urojona oraz moduł zespolony, aż wreszcie po takie w których występują potęgi i różne kombinacje wszystkich typów równań. Jakie są metody rozwiązywania równań zespolonych? Podstawą jest próba zapisania wszystkich liczb zespolonych występujących w równaniu w postaci elgebraicznej, a czasem w wykładniczej. Następnie korzystając z własności działań na liczbach zespolonych (dodawanie, odejmowanie, mnożenie i dzielenie) oraz w razie potrzeby z potęgowania zespolonego (wzór de Moivre'a) upraszczamy równanie. Często w ten sposób można otrzymać końcowe rozwiązanie, ale czasem trzeba użyć bardziej skomplikowanych metod, jak wzór na pierwiastkowanie zespolone lub schematy znajdowania pierwiastków wielomianów.