Start Wykonaj transponowanie macierzy:
\(A=\begin{bmatrix}2 &3 &1 &4\\{-1} &2 &0 &1\\ 2 &2 &0 &1 \end{bmatrix}\)
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Kategorie zadań z rozwiązaniami z matematyki wyższej
- Działania na macierzach (22)
- Wyznacznik macierzy (24)
- Macierz odwrotna (16)
- Równania macierzowe (14)
- Rząd macierzy (10)
- Wartości i wektory własne (4)
Macierze i wyznaczniki - zadania z rozwiązaniami
Wykonaj działania na macierzach:
\(\left(\left[\begin{array}{cc}1&0\\1&2\end{array}\right]^T-\left[\begin{array}{cc}0&2\\-1& 0\end{array}\right]\right)\cdot \left[\begin{array}{ccc}1&0&-1\\-1& 2&0\end{array}\right]\)
Wykonaj transponowanie macierzy A, następnie określ wymiar powstałej macierzy:
\(A=[1\,\, 2\,\, 3\,\, 4\,\, 5]\)
Wykonaj dodawanie macierzy:
\(\left[\begin{array}{ccc}1&-4&5\\0&2&-1\\4&2&1\\2&4&-6\end{array}\right]+\left[\begin{array}{ccc}3&1&2\\-2&0&1\\-3& 6&0\\-2&1&5\end{array}\right]\)
Wykonaj transponowanie macierzy:
\(A=\begin{bmatrix}1\\2\\3\\4\\5\end{bmatrix}\)
Wykonaj mnożenie macierzy przez liczbę:
\(2\cdot \begin{bmatrix} 2 & 3 & 1 & 4\\ -1 & 2 & 0 & 1\\ 2 & 2 & 0 & 1 \end{bmatrix}\)
Wykonaj mnożenie macierzy:
\(A=\begin{bmatrix} 1 & 0 & 2 \\ -1 & 3 & 1 \\ \end{bmatrix},\,\,\,B=\begin{bmatrix} 3 & 1 \\ 2 & 1 \\ 1 & 0 \end{bmatrix}\)
Wykonaj mnożenie macierzy:
\(\begin{bmatrix}1&2&3&4\end{bmatrix} \cdot \begin{bmatrix} 5\\6\\7\\8\end{bmatrix}\)
Wykonaj odejmowanie macierzy:
\(\left[\begin{array}{ccc}1&-4&5\\0& 2& -1\\4& 2&1\\2&4&-6\end{array}\right]-\left[\begin{array}{ccc}3&1&2\\-2&0&1\\-3& 6&0\\-2&1&5\end{array}\right]\)
Wykonaj mnożenie macierzy:
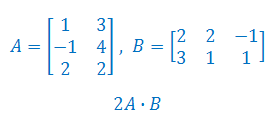
Wykonaj dodawanie macierzy A i B:
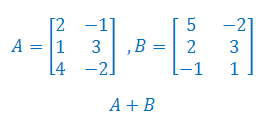
Korzystając z własności transponowania macierzy uzasadnij, że:
\((A-B)^T=A^T-B^T\)
Wykonaj mnożenie macierzy:
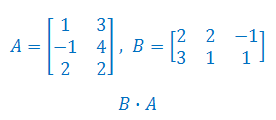
Wykonaj mnożenie macierzy:
\(\begin{bmatrix}1\\1\\1\\1\end{bmatrix} \cdot \begin{bmatrix} 1&1&1&1\end{bmatrix}\)
Podaj przykład macierzy, których mnożenie nie jest przemienne.
Znajdź wszystkie macierze przemienne z macierzą A:
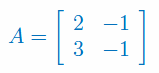
Wykonaj podane działania na macierzach A, B:
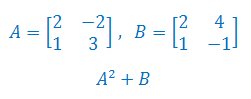
Wykonaj podane działania na macierzach A, B i C:
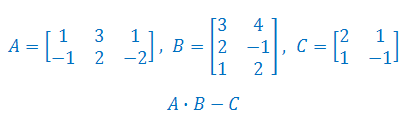
Dla jakich wartości parametrów \(a,b\in\mathbb{C}\) (liczby zespolone) prawdziwa jest równość macierzy:
\(\begin{bmatrix}a\\1\\0\end{bmatrix}\cdot \begin{bmatrix} a \\ b\\ a+b \end{bmatrix}^T=\begin{bmatrix}-1&1&0\\i&-i&0\\0&0&0\end{bmatrix}\)
Wykonaj mnożenie macierzy zespolonych:
\(\begin{bmatrix}i\\1\\0\end{bmatrix}\cdot \begin{bmatrix} i \\ -i\\ 0 \end{bmatrix}^T\)
Dla jakich wartości parametrów \(a,b\in\mathbb{R}\) prawdziwa jest równość macierzy:
\(\begin{bmatrix}a&2\\-2&b\end{bmatrix}\cdot \begin{bmatrix} 0 & 1 \\ 2 & 1 \end{bmatrix}=\begin{bmatrix}4&8\\3&2\end{bmatrix}^T\)
Wykonaj mnożenie macierzy:
\(\begin{bmatrix}22&-6&-26&17\\-17&5&20&-13\\-1&0&2&-1\\4&-1&-5&3\end{bmatrix}\cdot \begin{bmatrix}1&2&3&4\\2&3&1&2\\1&1&1&-1\\1&0&-2&-6\end{bmatrix}\)
oraz mnożenie w odwrotnej kolejności. Sprawdź czy \(A\cdot B=B\cdot A\)?
Oblicz wyznacznik macierzy diagonalnej:
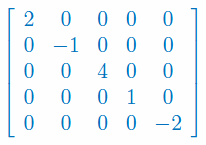
Oblicz wyznacznik macierzy 6x6:
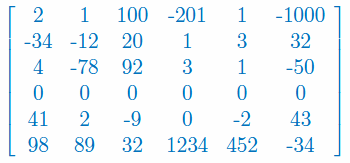
Wykonaj operacje elementarne \(w_1-\frac{1}{6}w_7\) oraz \(w_3+2w_4\) na wierszach macierzy
\(\begin{bmatrix}0&1&1&1&1&1&1\\1&1&0&0&0&0&0\\1&0&2&0&0&0&0\\1&0&0&3&0&0&0\\1&0&0&0&4&0&0\\1&0&0&0&0&5&0\\1&0&0&0&0&0&6\end{bmatrix}\)
Oblicz wyznacznik macierzy 3x3:
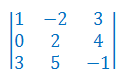
Stosując operacje elementarne oblicz wyznacznik macierzy:
\(\det\begin{bmatrix}1&2&3\\-4&1&0\\1&2&3\end{bmatrix}\)
Oblicz wyznacznik macierzy:
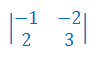
Oblicz wyznacznik macierzy metodą Sarrusa:
\(\det \begin{bmatrix}1&2&0\\-4&1&0\\-1&8&0\end{bmatrix}\)
Oblicz wyznacznik macierzy stopnia 2:
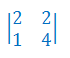
Stosując rozwinięcie Laplace'a oblicz wyznacznik macierzy 4x4:
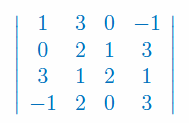
Podaj przykład macierzy, której wyznacznik jest równy 1.
Oblicz wyznacznik macierzy stopnia 3:
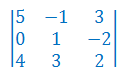
Stosując rozwinięcie Laplace'a udowodnić wzór na wyznacznik stopnia 2:
\(det\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}=a_{11}\cdot a_{22}-a_{12}\cdot a_{21}\)
Oblicz możliwe wartości wyznacznika macierzy spełniającej równanie:
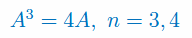
Oblicz wyznacznik macierzy zespolonej:
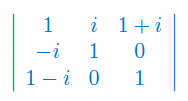
Oblicz wyznacznik macierzy \(C=A\cdot B\):
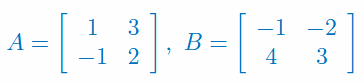
Oblicz wyznacznik macierzy \(C=A^{-1}\cdot B^T\):
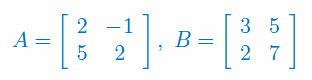
Znaleźć wartości x, które spełniają równanie z wyznacznikiem:
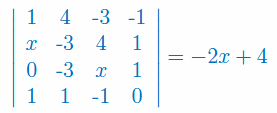
Oblicz wyznacznik macierzy 6x6:
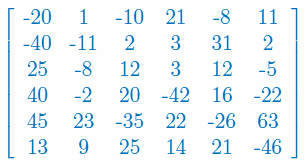
Oblicz wyznacznik macierzy:
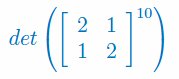
Oblicz wyznacznik macierzy i sprawdź czy macierz jest osobliwa:
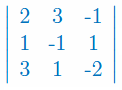
Stosując rozwinięcie Laplace'a oblicz wyznacznik macierzy wymiaru 4x4:
Oblicz wyznacznik macierzy trójkątnej:
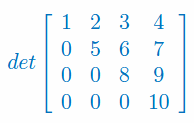
Stosując rozwinięcie Laplace'a oblicz wyznacznik macierzy stopnia 3:
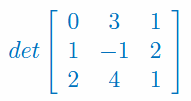
Oblicz wyznacznik macierzy stopnia 7:
\(\begin{bmatrix}0&1&1&1&1&1&1\\1&1&0&0&0&0&0\\1&0&2&0&0&0&0\\1&0&0&3&0&0&0\\1&0&0&0&4&0&0\\1&0&0&0&0&5&0\\1&0&0&0&0&0&6\end{bmatrix}\)
Oblicz macierz odwrotną do macierzy stopnia 2:
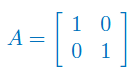
Oblicz macierz odwrotną przy użyciu metody Gaussa:
\(A=\begin{bmatrix}2&0\\3&1\end{bmatrix}\)
Oblicz macierz odwrotną do macierzy wymiaru 2x2:
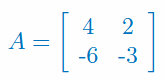
Oblicz dopełnienia algebraiczne wszystkich elementów macierzy:
\(\begin{bmatrix}0&-4\\1&2\end{bmatrix}\)
Jesteś w kategorii Macierze zadania z rozwiązaniami
W dziele "Macierze i wyznaczniki" masz do dyspozycji kilkadziesiąt przykładów i zadań z pełnymi rozwiązaniami z zakresu macierzy. Działy tematyczne obejmują najprostsze zagadnienia, takie jak działania na macierzach (transponowanie, dodawanie i odejmowanie, mnożenie macierzy), jak również trudniejsze tematy (liczenie wyznacznika, macierzy odwrotnej i rzędu macierzy) oraz zagadnienia, które są wymagane tylko na niektórych kierunkach studiów tj. wartości i wektory własne. Zadania w każdym dziale najczęściej uporządkowane są pod względem rosnącego poziomu trudności.
Niestety, nauka macierzy i wyznaczników (jak zresztą całej matematyki) jest jak domino, musisz dobrze opanować podstawowe zagadnienia, żeby móc opanować trudniejszy materiał, np. aby obliczyć macierz odwrotną musisz umieć liczyć wyznacznik macierzy oraz wykonywać transponowanie macierzy, aby liczyć wyznacznik musisz znać operacje elementarne na wierszach itd.
Warto próbować samodzielnie rozwiązać jak największą liczbę zadań z macierzy i sięgać do rozwiązań zamieszczonych na stronie jedynie w ramach podpowiedzi lub w celu sprawdzenia wyniku. Pod każdym zadaniem masz możliwość zadania pytania w komentarzu, warto z tej możliwości korzystać, ponieważ nie ma głupich pytań i na tej stronie żadne pytanie nie pozostanie bez odpowiedzi. Zachęcam do systematycznej nauki macierzy na przykładach, która przynosi zdecydowanie najlepsze efekty. Powodzenia w nauce macierzy!