Start 
Wyznacz dziedzinę i narysuj wykres funkcji
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Dziedzina i własności funkcji - zadania z rozwiązaniami
Określ dziedzinę funkcji (dla \(x\in\mathbb{R}\))
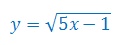
Określ dziedzinę funkcji
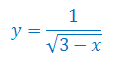
Określ dziedzinę funkcji
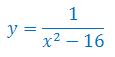
Oblicz miejsca zerowe funkcji
\(f(x)=\frac{(x-1)(x+2)}{\sqrt{x}-1}\)
Wyznacz dziedzinę, miejsca zerowe i zbiór wartości funkcji wymiernej
\(f(x)=\frac{2}{x+3}+4\)
Podaj przykład funkcji wymiernej, która dla argumentu równego 1 przyjmuje wartość 5, a jej dziedziną jest zbiór:
\(D_f=\mathbb{R}\setminus \{0\}\)
Podaj przykład funkcji, której dziedziną jest zbiór liczb rzeczywistych dodatnich.
Wyznacz dziedzinę funkcji
\(f(x)=\ln(|x|)+\frac{1}{x-1}\)
Wyznacz dziedzinę funkcji
\((a)\,\, f(x)=\ln(|x|+1)\)
\((b)\,\, f(x)=\ln(|x|-1)\)
Wyznacz dziedzinę funkcji
\(f(x)=\ln(|x|)\)
Oblicz miejsca zerowe wielomianu
\(f(x)=x^3-3x^2+2\)
Podaj przykład funkcji, której dziedziną jest przedział:
\([0,1]\)
Wyznacz dziedzinę funkcji
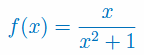
Wyznacz dziedzinę i narysuj wykres funkcji
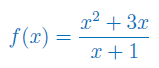
Wyznacz dziedzinę i narysuj wykres funkcji
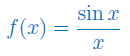
Wyznacz dziedzinę funkcji
Wyznacz dziedzinę funkcji
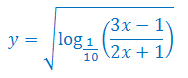
Wyznacz dziedzinę funkcji
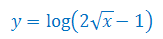
Wyznacz dziedzinę funkcji
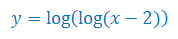
Wyznacz dziedzinę funkcji
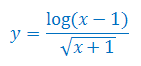
Wyznacz dziedzinę funkcji
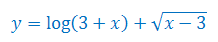
Wyznacz dziedzinę funkcji
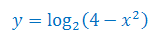
Wyznacz dziedzinę funkcji
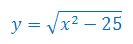
Wyznacz dziedzinę funkcji
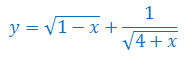
Wyznacz dziedzinę funkcji
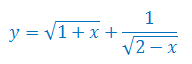
Jesteś w kategorii Dziedzina i własności funkcji zadania z rozwiązaniami
W tej kategorii znajdziesz kilkadzisiąt zadań i przykładów pokazujących jak wyznaczyć dziedzinę funkcji jednej zmiennej oraz jak określać własności funkcji takie jak monotoniczność, miejsca zerowe, czy zbiór wartości. W tym dziale poznasz również techniki rysowania wykresów funkcji.
Dziedzina funkcji tozbiór wszystkich argumentów funkcji, czyli zbiór tych x-ów dla których określona jest funkcja lub inaczej zbiór tych x-ów, dla których istnieje wykres funkcji.
Miejsca zerowe funkcji to takie argumenty x dla których funkcja przyjmuje wartości równe zero, czyli takie x, że \(f(x)=0\).
Funkcja jest monotoniczna, gdy jest rosnąca, malejąca lub stała.