Start 
Podaj sprzężenie liczby zespolonej oraz zaznacz je na płaszczyźnie zespolonej
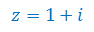
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Sprzężenie, moduł i argument zespolony - zadania
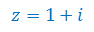
Wykaż, że:
\(z\cdot \overline{z}=|z|^2\)
Oblicz moduł i argument liczby zespolonej:
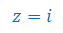
Oblicz sprzężenie i moduł liczby zespolonej:
\(-3+4i\)
Oblicz sprzężenie i moduł liczby zespolonej z:
\(z=-2i\)
Oblicz moduł i sprzężenie liczby zespolonej:
\(z=1\)
Oblicz moduł i argument liczby zespolonej oraz zaznacz je na płaszczyźnie zespolonej:
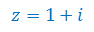
Oblicz moduł i argument liczby zespolonej oraz zaznacz je na płaszczyźnie zespolonej:
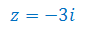
Oblicz moduł liczby zespolonej:
\(\left|\frac{\frac{\sqrt{3}}{2}+\frac{1}{2}i}{\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i}\right|\)
Oblicz moduł liczby zespolonej:
\(\big|(1+i)^{10}\cdot i^{2017}\big|\)
Wykaż, że:
\(|z_1\cdot z_2|=|z_1|\cdot |z_2|\)
Wykaż, że dla każdego \(n\in \mathbb{N}\):
\(|z^n|=|z|^n\)
Niech \(z\neq 0\), będzie pewną liczbą zespoloną. Która z liczb ma najmniejszy moduł:
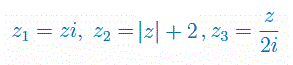
Oblicz moduł liczby zespolonej:
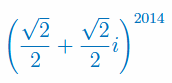
Oblicz moduł i argument liczby zespolonej:
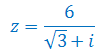
Oblicz moduł i argument liczby zespolonej:
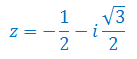
Udowodnij, że każda liczba zespolona \(z\neq -1\) o module równym 1 może być przedstawiona w postaci:
\(z=\frac{1+ti}{1-ti},\,\,\textrm{gdzie}\,\,t\in\mathbb{R}\)
Wykaż, że moduł liczby zespolonej \(z=\sin \alpha +\cos \alpha\, i\), \(\alpha\in\mathbb{R}\) jest równy 1.
Oblicz moduł i argument liczby zespolonej oraz zaznacz je na płaszczyźnie zespolonej:
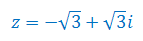
Niech \(\arg(z)=\frac{\pi}{4}\). Wyznacz argument główny liczb zespolonych:
\((a)\, z^2\)
\((b)\, z^3\)
\((c)\, z^{100}\)
Niech \(|z|=2\). Wyznacz moduły liczb zespolonych:
\((a)\, z^2\)
\((b)\, \frac{z^3}{2}\)
Wyznacz argumenty liczb zespolonych:
(a) \(\frac{\sqrt{3}}{2}+\frac{1}{2}i\)
(b) \(\frac{1}{2}+\frac{\sqrt{3}}{2}i\)
(c) \(-\frac{1}{2}+\frac{\sqrt{3}}{2}i\)
(d) \(-\frac{\sqrt{3}}{2}+\frac{1}{2}i\)
(e) \(-\frac{1}{2}-\frac{\sqrt{3}}{2}i\)
(f) \(\frac{1}{2}-\frac{\sqrt{3}}{2}i\)