Korzystając z definicji oblicz pochodną funkcji:
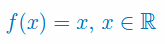
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Korzystając z definicji oblicz pochodną funkcji:
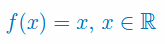
Korzystając z definicji oblicz pochodną funkcji:
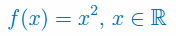
Korzystając z definicji oblicz pochodną funkcji:

Korzystając z definicji oblicz pochodną funkcji:
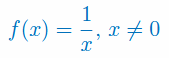
Korzystając z definicji oblicz pochodną funkcji:

Korzystając z definicji zbadaj czy istnieje pochodna funkcji w punkcie \(x_0=0\):
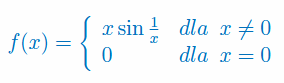
Korzystając z definicji (\(x\to x_0\)) oblicz pochodną funkcji:
\(f(x)=x^n,\,n\in\mathbb{N}\)
Korzystając z definicji wyprowadź wzór na pochodną iloczynu funkcji:
\((f(x)\cdot g(x))'=f'(x)g(x)+f(x)g(x)\)
Korzystając z definicji wyprowadź wzór na pochodną ilorazu funkcji:
\(\left(\frac{f(x)}{g(x)}\right )'=\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}\)
Korzystając z definicji zbadaj istnienie pochodnej funkcji \(f(x)=|x|\) w punkcie \(x_0=0\).
Korzystając z definicji oblicz pochodną funkcji wykładniczej:
\(f(x)=a^x,\,\,a>0\)
Korzystając z definicji (\(h\to 0\)) oblicz pochodną funkcji potęgowej:
\(f(x)=x^n,\,\,n\in\mathbb{N}\)
Korzystając z definicji oblicz pochodną funkcji sinus:
\(f(x)=\sin(x)\)
Korzystając z definicji oblicz pochodną funkcji cosinus:
\(f(x)=\cos(x)\)
Korzystając z definicji oblicz pochodną funkcji logarytmicznej:
\(f(x)=\log_a(x),\,a>0,\,a\neq 1,\,x>0\)
Korzystając z definicji oblicz pochodną funkcji sinus:
\(f(x)=\sin(x)+x^2-2x\)