Start 
Wyznacz przedział zbieżności szeregu:
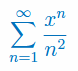
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Szeregi potęgowe i funkcyjne - zadania
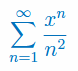
Korzystając z Tw. Weierstrassa uzasadnij zbieżność bezwzględną i jednostajną szeregu funkcyjnego:
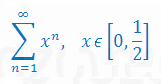
Wyznacz przedział zbieżności szeregu:
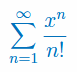
Wyznacz przedział zbieżności szeregu:
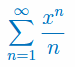
Wyznacz przedział zbieżności szeregu w zależności od parametru p:
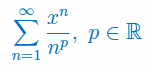
Wyznacz przedział zbieżności szeregu potęgowego:
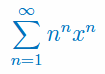
Wyznacz przedział zbieżności szeregu:
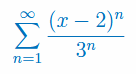
Wyznacz przedział zbieżności szeregu:
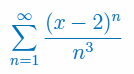
Wyznacz przedział zbieżności szeregu:
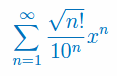
Korzystając z Tw. Weierstrassa uzasadnij zbieżność bezwzględną i jednostajną szeregu funkcyjnego:
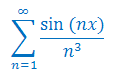
Korzystając z Tw. Weierstrassa uzasadnij zbieżność bezwzględną i jednostajną szeregu funkcyjnego:
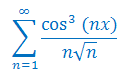
Korzystając z Tw. Weierstrassa uzasadnij zbieżność bezwzględną i jednostajną szeregu funkcyjnego dla \(x\ge 0\):
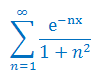
Korzystając z Tw. Weierstrassa uzasadnij zbieżność bezwzględną i jednostajną szeregu funkcyjnego:
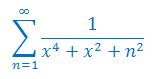
Zbadaj zbieżność jednostajną szeregu funkcyjnego:
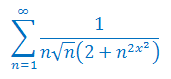
Zbadaj zbieżność jednostajną szeregu funkcyjnego:
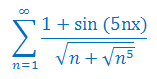
Zbadaj zbieżność jednostajną szeregu funkcyjnego:
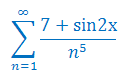
Zbadaj zbieżność jednostajną szeregu funkcyjnego dla \(x\ge 0\):
\(\sum\limits_{n=1}^\infty \frac{e^{-x}}{x+n^4}\)