Rozwiąż układ Cramera z 2 niewiadomymi:
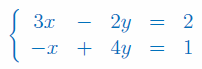
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Rozwiąż układ Cramera z 2 niewiadomymi:
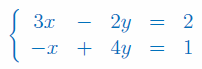
Rozwiąż układ równań liniowych z 2 niewiadomymi:
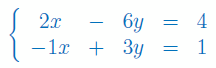
Rozwiąż układ Cramera z 3 niewiadomymi:
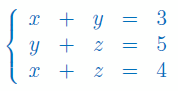
Stosując wzory Cramera wyznacz niewiadomą y
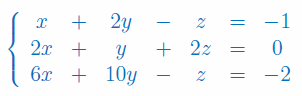
Zbadać dla jakich wartości parametru p układ równań jest układem Cramera. Następnnie wyznaczyć wartości niewiadomych
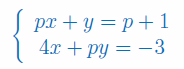
Rozwiązać układ równań metodą wyznacznikową:
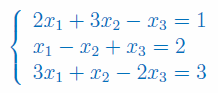
Inwestor chce kupić akcje za 100 tys. zł, chcąc uzyskać przeciętny (średni) zysk w ciagu pół roku na poziomie 13,5%, przy ryzyku w wysokości 10%. Doradca inwestycyjny oferuje mu 3 pakiety akcji o róznym średnim wzroście i ryzyku:
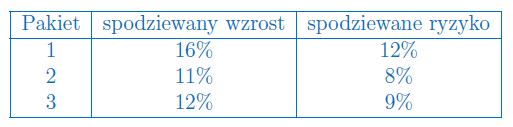
Jakie kwoty pieniędzy powinien zainwestować inwestor w akcjie z każdego pakietu, żeby zrealizować swój cel inwestycyjny?
Zbadaj liczbę rozwiązań układu równań w zależności od parametru p. Dla p=2, korzystając ze wzorów Cramera wyznacz wartość niewiadomej y:
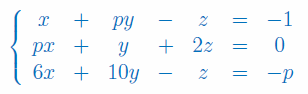
Rozwiąż układ równań z 2 niewiadomymi (x,y) metodą przeciwnych współczynników oraz za pomocą wzorów Cramera:
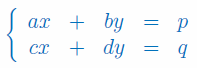
gdzie \(a,b,c,d,p,q\in\mathbb{R}\).
Dla jakich wartości parametru p układ równań jest układem Cramera:
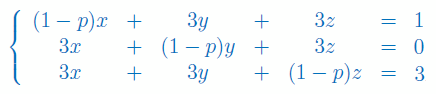
Rozwiąż układ równań stosując wzory Cramera
\(\left\{\begin{array}{ccccccc}x&+&y&+&z&=&5\\2x&+&2y&+&z&=&3\\3x&+&2y&+&z&=&1\end{array}\right.\)
Rozwiąż układ równań stosując wzory Cramera
\(\left\{\begin{array}{ccccccccc}x_1&+&x_2&+&x_3&+&x_4&=&4\\2x_1&+&x_2&-&x_3&+&3x_4&=&5\\5x_1&-&2x_2&+&x_3&+&x_4&=&5\\-x_1&+&x_2&+&3x_3&+&2x_4&=&5\end{array}\right.\)
Rozwiąż układ równań stosując wzory Cramera
\(\left\{\begin{array}{ccccccccccc}x_1&+&x_2&+&x_3&+&x_4&+&x_5&=&5\\2x_1&+&x_2&-&x_3&+&3x_4&+&x_5&=&6\\5x_1&-&2x_2&+&x_3&+&x_4&-&x_5&=&4\\-x_1&+&x_2&+&3x_3&+&2x_4&+&2x_5&=&7\\x_1&-&x_2&+&x_3&-&x_4&+&x_5&=&1\end{array}\right.\)
Jesteś w dziale Wzory Cramera zadania z rozwiązaniami
Wzory Cramera służą do rozwiązywania układów równań o takiej samej liczbie równań i niewiadomych oraz gdy macierz główna układu jest nieosobliwa (jej wyznacznik jest różny od zera). Aby zastosować wzory Cramera należy zapisać macierz główną układu i obliczyć jej wyznacznik. Jeśli wyznacznik macierzy głównej jest różny od zera, to układ równań jest układem Cramera. Teraz należy zapisać macierze powstałe przez zastąpienie kolumn w macierzy głównej kolumną wyrazów wolnych. Następnie należy obliczyć wyznaczniki tych macierzy i otrzymane wartości podstawić do wzorów Cramera.
W tym dziale znajdziesz wiele zadań i przykładów pokazujących jak stosować wzory Cramera do rozwiązywania układów równań liniowych o takiej samej liczbie równań i niewiadomych. Jeśli będziesz mieć problem ze zrozumieniem jakiegoś fragmentu rozwiązania, to zachęcam do zadawania pytań z komentarzach.