Start 
Dla jakich wartości parametrów \(a,b\in\mathbb{R}\) prawdziwa jest równość macierzy:
\(\begin{bmatrix}a&2\\-2&b\end{bmatrix}\cdot \begin{bmatrix} 0 & 1 \\ 2 & 1 \end{bmatrix}=\begin{bmatrix}4&8\\3&2\end{bmatrix}^T\)
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Równania macierzowe - zadania z rozwiązaniami
Dla jakich wartości parametrów \(a,b\in\mathbb{C}\) (liczby zespolone) prawdziwa jest równość macierzy:
\(\begin{bmatrix}a\\1\\0\end{bmatrix}\cdot \begin{bmatrix} a \\ b\\ a+b \end{bmatrix}^T=\begin{bmatrix}-1&1&0\\i&-i&0\\0&0&0\end{bmatrix}\)
Korzystając z definicji równości macierzy wyznacz liczby a,b,c,d
\(\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}\)
Korzystając z definicji równości macierzy rozwiąż równanie macierzowe (znajdź a i b)
\({\begin{bmatrix} a & -2 & 1+a \\ b+1 & 0 & 1\\ a+b & 1 &b \end{bmatrix}=\begin{bmatrix} a & a-b& b-1\\ b+1 & a+b& b\\0&1&-a \end{bmatrix}}\)
Rozwiąż równanie macierzowe:
\(2A+3X=B\)
gdzie A i B są dowolnymi macierzami stopnia n.
Znajdź macierz X spełniającą równanie macierzowe:
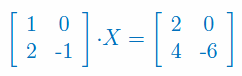
Znajdź wszystkie macierze X spełniające równanie macierzowe:
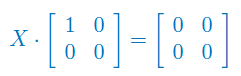
Znajdź macierz X spełniającą równanie macierzowe:
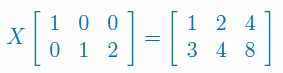
Znajdź macierz X spełniającą równanie macierzowe:
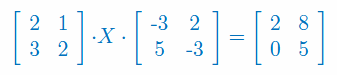
Wyznacz elementy macierzy X, jeżeli:
\(2X\begin{bmatrix} -1 & 1 \\1 & -2\end{bmatrix}^T+5I=\begin{bmatrix} 3 & 1\\ 1&2\end{bmatrix}\begin{bmatrix}3&-5\\-2&4\end{bmatrix}^T\)
Rozwiąż równanie macierzowe:
\(\begin{bmatrix} -1 & 2 \\1 & 0\end{bmatrix}\cdot (X+I)=\begin{bmatrix} -1 & 2\\ 1&0\end{bmatrix}\cdot X-X\)
Rozwiąż równanie macierzowe:
\(\begin{bmatrix}1&-3\\2&-2\\3&-1\end{bmatrix}^T\begin{bmatrix}0&-1\\-1&1\\1&0\end{bmatrix}-2\left(\begin{bmatrix}-2&4\\-1&2\end{bmatrix}^2+X\right)=(X^T+I^2)^T\)
Rozwiąż równanie macierzowe:
\(A\cdot X\cdot A^{-1}=I\)
gdzie A jest dowolną macierzą nieosobliwą stopnia n, a I to macierz jednostkowa stopnia n.
Rozwiąż równanie macierzowe:
\(A^{-1}\cdot X\cdot C^{-1}=B\)
gdzie B, C to macierze nieosobliwe stopnia 3, takie, że \(B\cdot C=A^2\) oraz:
\(A=\begin{bmatrix}1&0&0\\0&2&0\\0&0&3\end{bmatrix}\)
Rozwiąż równanie macierzowe:
\(A\cdot B=I\)
gdzie A jest macierzą wymiaru 1x2, a B macierzą o wymiarach 2x1 (I jest macierzą jednostkową).
Wyznacz elementy macierzy X, jeżeli:
\(X\cdot \begin{bmatrix}1&2&3&4\\2&3&1&2\\1&1&1&-1\\1&0&-2&-6\end{bmatrix}=\begin{bmatrix}1&0&0&1\\0&0&1&0\\0&1&0&0\\1&0&0&0\end{bmatrix}\)