Start Podaj część rzeczywistą i urojoną liczby zespolonej z:
\(z=-6\)
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Kategorie zadań z rozwiązaniami z matematyki wyższej
Liczby zespolone - zadania z rozwiązaniami
Oblicz:
\(i+2i\)
Wykonaj działania na liczbach zespolonych:
\(\frac{1}{2}+i-\left(2+\frac{1}{2}i\right)\)
Wykonaj dzielenie liczb zespolonych:
\(\frac{1}{i}\)
Podaj część rzeczywistą i urojoną liczby zespolonej z:
\(z=2i\)
Wykonaj dzielenie:
\(\frac{1}{z}\)
wiedząc, że \(z=x+yi\), gdzie \(x,y\in\mathbb{R}\).
Wykonaj dzielenie liczb zespolonych:
\(\frac{1}{1+i}\)
Podaj część rzeczywistą i urojoną liczby zespolonej z:
\(z=2-i\)
Wykonaj mnożenie liczb zespolonych:
\((3-\sqrt{2}i)(-1-i)\)
Wykonaj potęgowanie jednostki urojonej:
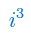
Wykonaj potęgowanie jednostki urojonej:
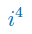
Wykonaj potęgowanie jednostki urojonej:
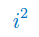
Wykonaj działania na liczbach zespolonych:
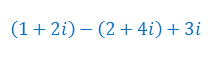
Wykonaj działanie na liczbach zespolonych:
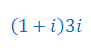
Wykonaj mnożenia liczb zespolonych:
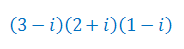
Oblicz potęgę liczby zespolonej:
\((2-i)^2\)
Wykonaj potęgowanie:
\((1-i)^3\)
Oblicz potęgę liczby zespolonej:
\((1+i)^8\)
Wykonaj potęgowanie jednostki urojonej:
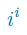
Wykonaj potęgowanie jednostki urojonej:
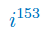
Wykonaj potęgowanie jednostki urojonej:
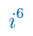
Wykonaj potęgowanie jednostki urojonej:
Podaj część rzeczywistą i urojoną liczby zespolonej:
\(z=\frac{1}{1-i}\)
Oblicz
\(\frac{1}{1-i}-\frac{1}{1+i}\)
Oblicz
\(\frac{1}{z}+\frac{1}{\overline{z}}\)
gdzie \(z\) jest liczbą zespoloną.
Niech \(z=x+yi\), \(x,y\in\mathbb{R}\). Wyznacz część rzeczywistą i urojoną liczby zespolonej:
\(z^2\)
Podaj część rzeczywistą i urojoną liczby zespolonej:
\(z=\frac{1-i}{1+i}\)
Podaj część rzeczywistą i urojoną liczby zespolonej:
\(z=\frac{1+i}{1-i}\)
Wykonaj dzielenie liczb zespolonych:
\(\frac{(1+i)^2-2i^3}{(1-i)(1+i)}\)
Oblicz
\(\frac{1}{z}-\frac{1}{\overline{z}}\)
gdzie \(z\) jest liczbą zespoloną.
Niech \(z=x+yi\), \(x,y\in\mathbb{R}\). Wyznacz część rzeczywistą i urojoną liczby zespolonej:
\(\frac{1}{z+i}\)
Oblicz
\(\frac{1}{1-i}+\frac{1}{1+i}\)
Niech \(z=x+yi\), \(x,y\in\mathbb{R}\). Jaka jest część rzeczywista i urojona liczby zespolonej:
\(z^3\)
Wykonaj dzielenie liczb zespolonych:
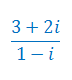
Wykonaj działania na liczbach zespolonych:
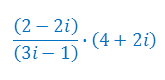
Wykonaj dzielenie liczb zespolonych:
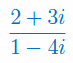
Wykonaj działania na liczbach zespolonych:
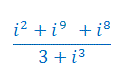
Wykonaj dzielenie liczb zespolonych:
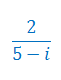
Wykonaj działania na liczbach zespolonych:
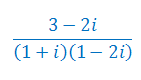
Wykonaj działania na liczbach zespolonych:
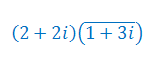
Korzystając ze wzoru de Moivre'a oblicz potęgę:
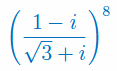
Korzystając ze wzoru de Moivre'a oblicz potęgę:
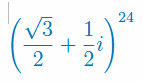
Podaj sprzężenie liczby zespolonej oraz zaznacz je na płaszczyźnie zespolonej
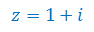
Wykaż, że:
\(z\cdot \overline{z}=|z|^2\)
Oblicz moduł i argument liczby zespolonej:
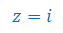
Oblicz moduł i sprzężenie liczby zespolonej:
\(z=1\)
Oblicz sprzężenie i moduł liczby zespolonej z:
\(z=-2i\)
Oblicz sprzężenie i moduł liczby zespolonej:
\(-3+4i\)
Oblicz moduł i argument liczby zespolonej oraz zaznacz je na płaszczyźnie zespolonej:
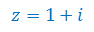
Oblicz moduł i argument liczby zespolonej oraz zaznacz je na płaszczyźnie zespolonej:
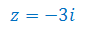
Jesteś w kategorii Liczby zespolone zadania z rozwiązaniami
Znajdziesz tutaj przykłady i zadania z rozwiązaniami krok po kroku z zakresu liczb zespolonych. Działy tematyczne obejmują najprostsze zagadnienia, takie jak działania na liczbach zespolonych (dodawanie, odejmowanie, mnożenie i dzielenie), metody obliczania modułu i argumentu zespolonego oraz bardziej skompliowane zagadnienia, takie jak potęgowanie liczb zespolonych (wzór de Moivre'a), równania zespolone, metody obliczania pierwiastków zespolonych oraz rysowanie zbiorów na płaszczyźnie zespolonej. Zadania najczęścieij uporządkowane są pod względem rosnącego poziomu trudności.
Na stronie obliczone.pl będziesz uczyć się liczb zespolonych na przykładach, co pozwoli Ci opanować materiał dużo szybciej i efektywniej. Wystarczy pracować systematycznie i starać się przeanalizować ze zrozumieniem jak najwięcej zadań, warto również rozwiązywać zadania samodzielnie i w razie problemów sięgać po podpowiedź. W przypadku, gdy będziesz mieć problem ze zrozumieniem jakiegoś fragmentu rozwiązania zachęcam do zadawania pytań w komentarzu pod zadaniem. Nawet najbanalniejsze pytanie nie pozostanie bez odpowiedzi. Na koniec nie pozostaje mi nic innego jak tylko życzyć Ci udanej nauki liczb zespolonych i sukcesu na kolokwium, czy też egzaminie. Powodzenia!