Wykonaj potęgowanie jednostki urojonej
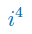
Rozwiązanie

UWAGI
We wszelkich obliczeniach na liczbach zespolonych stosuj definicję jednostki urojonej, tj.:
Jednostką urojoną nazywamy liczbę \(i\), taką, że \[i^2=-1\]
Jednostka urojona to formalnie jeden z dwóch elementów zbioru liczb zespolonych spełniających warunek \(i^2=-1\), drugim elementem jest liczba \(-i\), ponieważ \((-i)^2=(-1)^2\cdot i^2=-1\).
Często możesz spotkać się z zapisem
\[i=\sqrt{-1}\]
który choć nieformalny (czyli niepoprawny matematycznie) jest akceptowalny. Musisz jednak zachować ostrożność!
Do czego może prowadzić stosowanie zapisu \(i=\sqrt{-1}\)?
Oto przykłady sprzeczności jakie możena otrzymać stosując zapis \(i=\sqrt{-1}\):
\[-1=i^2=i\cdot i=\sqrt{-1}\sqrt{-1}=\sqrt{(-1)\cdot (-1)}=\sqrt{1}=1\]
\[\frac{1}{i}=\frac{\sqrt{1}}{\sqrt{-1}}=\sqrt{\frac{1}{-1}}=\sqrt{\frac{-1}{1}}=\sqrt{-1}=i\]
WAŻNE: Przy rozwiązywaniu zadań nie zamieniaj symbolu \(i\) na \(\sqrt{-1}\), jeśli jest "i" to niech tak zostanie, ale jeśli masz \(i^2\), \(i^3\) itp. to już spokojnie możesz zastosować definicję i napisać \(i^2=-1\) lub np. \(i^3=i^2\cdot i=-1\cdot i=-i\).

Komentarzy (0)