Start 
Wykonaj działania na macierzach:
\(\left(\left[\begin{array}{cc}1&0\\1&2\end{array}\right]^T-\left[\begin{array}{cc}0&2\\-1& 0\end{array}\right]\right)\cdot \left[\begin{array}{ccc}1&0&-1\\-1& 2&0\end{array}\right]\)
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Działania na macierzach - zadania z rozwiązaniami
Wykonaj transponowanie macierzy A, następnie określ wymiar powstałej macierzy:
\(A=[1\,\, 2\,\, 3\,\, 4\,\, 5]\)
Wykonaj transponowanie macierzy:
\(A=\begin{bmatrix}1\\2\\3\\4\\5\end{bmatrix}\)
Wykonaj transponowanie macierzy:
\(A=\begin{bmatrix}2 &3 &1 &4\\{-1} &2 &0 &1\\ 2 &2 &0 &1 \end{bmatrix}\)
Wykonaj mnożenie macierzy:
\(\begin{bmatrix}1&2&3&4\end{bmatrix} \cdot \begin{bmatrix} 5\\6\\7\\8\end{bmatrix}\)
Wykonaj mnożenie macierzy:
\(A=\begin{bmatrix} 1 & 0 & 2 \\ -1 & 3 & 1 \\ \end{bmatrix},\,\,\,B=\begin{bmatrix} 3 & 1 \\ 2 & 1 \\ 1 & 0 \end{bmatrix}\)
Wykonaj mnożenie macierzy przez liczbę:
\(2\cdot \begin{bmatrix} 2 & 3 & 1 & 4\\ -1 & 2 & 0 & 1\\ 2 & 2 & 0 & 1 \end{bmatrix}\)
Wykonaj dodawanie macierzy:
\(\left[\begin{array}{ccc}1&-4&5\\0&2&-1\\4&2&1\\2&4&-6\end{array}\right]+\left[\begin{array}{ccc}3&1&2\\-2&0&1\\-3& 6&0\\-2&1&5\end{array}\right]\)
Wykonaj odejmowanie macierzy:
\(\left[\begin{array}{ccc}1&-4&5\\0& 2& -1\\4& 2&1\\2&4&-6\end{array}\right]-\left[\begin{array}{ccc}3&1&2\\-2&0&1\\-3& 6&0\\-2&1&5\end{array}\right]\)
Wykonaj mnożenie macierzy:
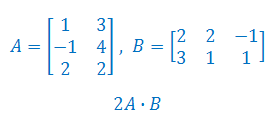
Korzystając z własności transponowania macierzy uzasadnij, że:
\((A-B)^T=A^T-B^T\)
Wykonaj mnożenie macierzy:
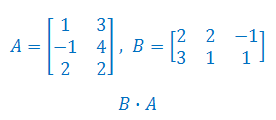
Wykonaj dodawanie macierzy A i B:
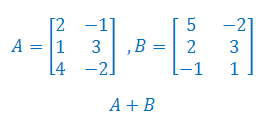
Wykonaj mnożenie macierzy:
\(\begin{bmatrix}1\\1\\1\\1\end{bmatrix} \cdot \begin{bmatrix} 1&1&1&1\end{bmatrix}\)
Podaj przykład macierzy, których mnożenie nie jest przemienne.
Znajdź wszystkie macierze przemienne z macierzą A:
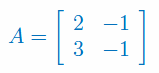
Wykonaj podane działania na macierzach A, B:
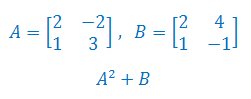
Wykonaj podane działania na macierzach A, B i C:
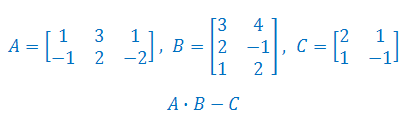
Dla jakich wartości parametrów \(a,b\in\mathbb{R}\) prawdziwa jest równość macierzy:
\(\begin{bmatrix}a&2\\-2&b\end{bmatrix}\cdot \begin{bmatrix} 0 & 1 \\ 2 & 1 \end{bmatrix}=\begin{bmatrix}4&8\\3&2\end{bmatrix}^T\)
Dla jakich wartości parametrów \(a,b\in\mathbb{C}\) (liczby zespolone) prawdziwa jest równość macierzy:
\(\begin{bmatrix}a\\1\\0\end{bmatrix}\cdot \begin{bmatrix} a \\ b\\ a+b \end{bmatrix}^T=\begin{bmatrix}-1&1&0\\i&-i&0\\0&0&0\end{bmatrix}\)
Wykonaj mnożenie macierzy zespolonych:
\(\begin{bmatrix}i\\1\\0\end{bmatrix}\cdot \begin{bmatrix} i \\ -i\\ 0 \end{bmatrix}^T\)
Wykonaj mnożenie macierzy:
\(\begin{bmatrix}22&-6&-26&17\\-17&5&20&-13\\-1&0&2&-1\\4&-1&-5&3\end{bmatrix}\cdot \begin{bmatrix}1&2&3&4\\2&3&1&2\\1&1&1&-1\\1&0&-2&-6\end{bmatrix}\)
oraz mnożenie w odwrotnej kolejności. Sprawdź czy \(A\cdot B=B\cdot A\)?