Całki nieoznaczone - podstawowe wzory i własności

1. Oznaczenia i przykłady całek

Całkę nieoznaczoną z funkcji f(x) zapisuje się symbolem:

\[\int\limits f(x)\,dx\]

Przykłady

\[\int x\,dx,\,\,\,\int \ln{x}\,dx,\,\,\,\int \frac{\sin{x}}{e^x}\,dx\]

UWAGA: Całki nieoznaczone i oznaczone są jednymi z ważniejszych działów analizy matematycznej. Jeśli masz mało czasu na naukę to zaglądnij od razu do działu analiza matematyczna w zadaniach.

2. Jak liczyć całki nieoznaczone?

Całkowanie jest operacją odwrotną do liczenia pochodnej funkcji, dlatego, żeby całkować trzeba umieć liczyć pochodne.

Jeżeli g(x) jest pochodną funkcji f(x), czyli

\[f'(x)=g(x)\]

to

\[\int g(x)\,dx=f(x)\]

funkcję f(x) nazywa się funkcją pierwotną funkcji g(x).

Jeżeli c jest dowolną liczbą rzeczywistą, to oczywiście

\[(f(x)+c)'=g(x)\]

dlatego przy wyniku całki należy dopisać stałą c:

\[\int g(x)\,dx=f(x)+c\]

UWAGA: Do wyniku całki nieoznaczonej dopisujemy zawsze stałą c.

Przykłady

\[(\sin x)'=\cos x\]

i ogólniej

\[(\sin x+c)'=\cos x\]

dlatego

\[\int \cos x\,dx=\sin x+c\]

Podobnie

\[(\ln x)'=\frac{1}{x}\]

i ogólniej

\[(\ln x+c)'=\frac{1}{x}\]

dlatego

\[\int \frac{1}{x}\,dx=\ln x+c\]

ZASADA 1: Jeśli chcesz policzyć całkę z funkcji g(x), musisz znaleźć funkcję f(x), której pochodna jest równa g(x). Pamiętaj, aby zawsze do wyniku całki nieoznaczonej dopisać stałą c (jak wyżej).

3. Całka z iloczynu dowolnej liczby przez funkcję

Jeżeli a jest liczbą rzeczywistą, to

\[\int af(x)\,dx=a\int f(x)\,dx\]

Przykład

4. Całka z sumy lub różnicy funkcji

jest sumą lub różnicą całek. Niech a i b będą dowolnymi liczbami rzeczywistymi, wtedy

\[\int \big(a\cdot f(x)\pm b\cdot g(x)\big)\,dx=a\int f(x)\,dx\pm b\int g(x)\,dx\]

ZASADA 2: Najłatwiej liczyć całki rozbijając je na sumę/różnicę "łatwiejszych" całek oraz wyciągając wszystkie stałe (liczby) przed całkę.

Całkowanie jest operacją liniową, innymi słowy całka z sumy lub różnicy funkcji pomnożonych przez dowolne stałe jest sumą lub różnicą całek pomnożonych przez te stałe.

5. Wzory na całki funkcji elementarnych

Poniższe wzory można wyprowadzić korzystając z faktu, że całkowanie jest operacją odwrotną do różniczkowania (liczenia pochodnej):

\[\int 0\, dx=0+c\]

bo \((0+c)'=0\)

\[\int 1\, dx=x+c\]

bo \((x+c)'=1\)

\[\int x\, dx=\frac{x^2}{2}+c\]

bo \(\left(\frac{x^2}{2}+c\right)'=2\frac{x}{2}=x\)

\[\int x^n\, dx=\frac{x^{n+1}}{n+1}+c,\,\,n\neq -1\]

bo \(\left(\frac{x^{n+1}}{n+1}+c\right)'=(n+1)\frac{x^n}{n+1}=x^n\)

UWAGA: Trzy pierwsze wzory wynikają z ostatniego ogólnego wzoru na całkę funkcji potęgowej (zastanów się jak?) i ten 4 wzór wystarczy zapamiętać.

5.1. Całki z logarytmami

\[\int x^{-1}\, dx=\ln |x|+c\]

\[\int \frac{dx}{ax+b}\, dx=\frac{1}{a}\ln|ax+b|+c,\,\,\,a\neq 0\]

\[\int \log_a x\, dx=\frac{x(\ln x-1)}{\ln a}+c,\,\,a>0,\,a\neq 1,\,x>0\]

Całka z \(\ln x\) nie jest tak banalna jak się wydaje, bo do jej policzenia potrzebna nam będzie metoda całkowania przez części (o której dowiesz się w dalszej części).

5.2. Całki z funkcji wykładniczych

\[\int a^x\, dx=\frac{a^x}{\ln a}+c,\,\,\,a>0\]

\[\int e^x\, dx=e^x+c\]

\[\int e^{kx}\, dx=\frac{1}{k}e^{kx}+c,\,\,\,k\neq 0\]

\[\int e^{-x}\, dx=-e^{-x}+c\]

5.3. Całki z funkcji trygonometrycznych

Całka z sinusa i cosinusa:

\[\int \sin x\, dx=-\cos x+c\]

\[\int \cos x\, dx=\sin x+c\]

Całka z tangensa i cotangensa

\[\int tg x\, dx=-\ln|\cos x|+c\]

\[\int ctg x\, dx=\ln|\sin x|+c\]

\[\int \frac{1}{\cos^2 x}\, dx=tgx+c\]

\[\int \frac{1}{\sin^2 x}\, dx=-ctgx+c\]

Wideo lekcja z całek funkcji trygonometrycznych

5.4. Całki z funkcjami cyklometrycznymi

\[\int \frac{1}{1+x^2}\, dx=arctg x+c\]

\[\int -\frac{1}{1+x^2}\, dx=arcctg x+c\]

\[\int \frac{1}{\sqrt{1-x^2}}\, dx=\arcsin x+c\]

\[\int -\frac{1}{\sqrt{1-x^2}}\, dx=\arccos x+c\]

Zobacz wyjaśnienia skąd się biorą wzory na całki

5.5. Wzory rekurencyjne na całki potęg funkcji trygonometrycznych

Jeżeli \(n\in\mathbb{N}\), to

\[\int \sin^n (x)\, dx=-\frac{1}{n}\sin^{n-1} (x)\cos (x)+\frac{n-1}{n}\int \sin^{n-2}(x)\,dx\]

\[\int \cos^n (x)\, dx=\frac{1}{n}\cos^{n-1} (x)\sin (x)+\frac{n-1}{n}\int \cos^{n-2}(x)\,dx\]

\[\int tg^n (x)\, dx=\frac{1}{n-1}tg^{n-1} (x)-\int tg^{n-2}(x)\,dx\]

\[\int ctg^n (x)\, dx=-\frac{1}{n-1}ctg^{n-1} (x)-\int ctg^{n-2}(x)\,dx\]

Powyższe wzory można wykorzystać do liczenia dowolnych potęg naturalnych funkcji trygonometrycznych, np. \(\int \sin^2 x\,dx,\, \int \sin^3 x\,dx, \,\int \cos^2 x\,dx\) itp.

Przykład

\[\int \sin^2 (x)\, dx=-\frac{1}{2}\sin (x)\cos (x)+\frac{1}{2}\int \sin^{0}(x)\,dx=\]\[=-\frac{1}{2}\sin(x)\cos(x)+\frac{1}{2}\int 1\,dx=-\frac{1}{2}\sin(x)\cos(x)+\frac{1}{2}x+c\]

5.6. Wzory na całki z pochodną funkcji

Jeżeli funkcja f(x) ma pochodną, to

\[\int f'(x)\, dx=f(x)+c\]

\[\int f(x)g'(x)\, dx=f(x)g(x)-\int f'(x)g(x)\,dx\]

\[\int f(g(x))g'(x)\, dx=\int f(x)\,dx\]

\[\int \frac{f'(x)}{f(x)}\, dx=\ln|f(x)|+c,\,\,\,f(x)\neq 0\]

\[\int \frac{f'(x)}{2\sqrt{f(x)}}\,dx=\sqrt{f(x)}+c,\,\,\,f(x)>0\]

\[\int f'(x)e^{f(x)}\, dx=e^{f(x)}+c\]

UWAGA: Pierwszy wzór wynika wprost z definicji całki (operacja odwrotna do różniczkowania). Drugi wzór to schemat całkowania przez części. Trzeci wzór to całkowanie przez podstawienie. Natomiast trzy ostatnie wzory można wyprowadzić korzystając z całkowania przez podstawienie.

Przykład

Stosując 4 (lub 3) wzór mamy:

\[\int \frac{2x}{x^2+1}\, dx=\int \frac{(x^2+1)'}{x^2+1}\,dx=\ln|x^2+1|+c\]

6. Metody całkowania

6.1. Metoda przez "odgadywanie"

polega na wykorzystaniu definicji całki (jako operacji odwrotnej do różniczkowania) i odgadnięciu wyniku, czyli funkcji, której pochodna jest równa funkcji podcałkowej. Metoda ta wymaga biegłości w liczeniu pochodnych i sprawdza się tylko w przypadku prostych całek, np. łatwo możemy odgadnąć wynik całki \(\int e^{2x}\, dx\) wiedząc, że \((e^x)'=e^x\):

\[\int e^{2x}\, dx=\frac{1}{2}e^{2x} +c\]

ponieważ

\[\left(\frac{1}{2}e^{2x} +c\right)'=\frac{1}{2}(e^{2x})'+(c)'=\frac{1}{2}\cdot 2 e^{2x}=e^{2x}\]

6.2. Całkowanie przez części

najczęściej można wykorzystać, gdy pod całką występuje iloczyn funkcji.

Jeżeli funkcje u(x) i v(x) mają ciągłe pochodne, to

\[\int u(x)v'(x)\, dx=u(x)v(x)-\int u'(x)v(x)\,dx\]

Przykład

Zwróć uwagę, że do całkowania przez części w wielu przypadkach możesz wykorzystać "jedynkę"
np. gdy zauważysz, że \(\ln x=1\cdot \ln x\), to dalej całkowanie pójdzie już gładko:

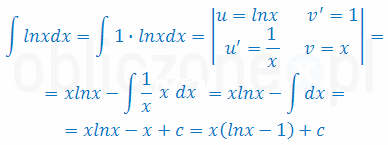
Lekcja wideo z całkowania przez części z przykładami:

Więcej przykładów całkowania przez części

6.3. Całkowanie przez podstawienie

najczęściej można wykorzystać, gdy pod całką występuje funkcja złożona i iloczyn funkcji.

Jeżeli funkcja g(x) ma ciągłą pochodną i

\[\int f(x)\,dx=F(x)+c\]

to

\[\int f(g(x))g'(x)\, dx=\left|\begin{array}{c}Podstawiamy:\\ g(x)=t\\ g'(x)dx=dt\end{array}\right|=\int f(t)dt=F(t)+c=F(g(x))+c\]

Przykład 1

Kluczem do opanowania metody całkowania przez podstawienie jest umiejętność szybkiego liczenia pochodnych funkcji, która pomoga określić jakie podstawienie należy wykonać:

Przykład 2

Odpowiednie podstawienie redukuje całkę do prostszej postaci:

Przykład 3

Poniższy wzór możesz potraktować jako schemat, który działa dla wszystkich funkcji \(f(x)\) określonych na zbiorze tych x, dla których \(f(x)\neq 0\):

\[\int \frac{f'(x)}{f(x)}\, dx=\left|\begin{array}{c}Podstawiamy:\\f(x)=t\\f'(x)dx=dt \end{array}\right|=\int \frac{1}{t}\,dt=\ln|t|+c=\ln|f(x)|+c\]

Lekcja wideo z całkowania przez podstawienie z przykładami:

Więcej przykładów całkowania przez podstawienie

ZASADA 3: Do liczenia całek niezbędne są różne metody całkowania, trzy najważniejsze to "odgadywanie" (sprawdza się w przypadku prostych całek), całkowanie przez części (przydaje się, gdy pod całką występuje iloczyn funkcji), całkowanie przez podstawienie (gdy pod całką występują funkcje złożone postaci f(g(x)) i iloczyny funkcji).

7. Przykłady całek, których nie można wyrazić za pomocą funkcji elementarnych

Nie każdą całkę da się przedstawić za pomocą znanych funkcji (np. wielomianu, logarytmu itp.)

\[\int e^{-x^2}\, dx,\,\,\,\int \frac{\sin x}{x}\, dx,\,\,\,\int x^x\,dx,\,\,\,\int \frac{1}{\ln x}\,dx\]

CIEKAWOSTKA: Istnieją całki, których w praktyce nie jeteśmy w stanie obliczyć podając zwięzły wzór (choć czasami można zapisać daną całkę za pomocą funkcji specjalnych).

8. Najczęściej popełniane błędy przy liczeniu całek

Poniższe wzory nie są prawdziwe i nie możesz ich stosować

Całka iloczynu funkcji NIE JEST iloczynem całek

\[\int f(x)\cdot g(x)\,dx \neq \int f(x)\,dx\cdot \int g(x)\,dx\]

Całka ilorazu funkcji NIE JEST ilorazem całek

\[\int \frac{f(x)}{g(x)}\,dx \neq \frac{\int f(x)\,dx}{\int g(x)\,dx}\]

9. Jak liczyć całki w kalkulatorze wolframalpha.com?

Jeśli chcesz sprawdzić wynik całki nieoznaczonej, to wystarczy, że wpiszesz w okienku na stronie wolframalpha.com komendę integrate i wzór funkcji, której całkę chcesz obliczyć, np. integrate ln(x)

Symbole, których można używać w wolframie:

+ - dodawanie

- - odejmowanie

* (lub nic) - mnożenie, np. 2x i 2*x

/ - dzielenie, np. x/(x+1) oznacza \(\frac{x}{x+1}\)

^ - potęgowanie, np. x^2 oznacza \(x^2\)

Przykłady zapisu funkcji w wolframie:

\(\frac{x^2}{x^3+2x+1}\rightarrow\) x^2/(x^3+2x+1)

\(\sin^4(3x)\rightarrow\) sin^4(3x)

Wynik całkowania możesz również sprawdzić w kalkulatorze całek nieoznaczonych mojego autorstwa. Kalkulator wyświetla wskazówki pomocne w liczeniu całek.

10. Podsumowanie - zapamiętaj 3 zasady ułatwiające całkowanie funkcji

1. Całkowanie jest operacją odwrotną do liczenia pochodnej funkcji (różniczkowania). Jeśli chcesz policzyć całkę z funkcji f(x), musisz znaleźć funkcję g(x), której pochodna jest równa f(x). Musisz najpierw opanować pochodne, żeby w ogóle myśleć o nauce całek.
2. Całkę sumy/różnicy funkcji możesz rozbić na sumę/różnicę całek, a liczby możesz wyciągać przed znak całki.
3. Do obliczania całek stosuj metody całkowania, z których najważniejsze to metoda "odgadywania" oraz całkowanie przez części i przez podstawienie.
4. Całka iloczynu funkcji NIE JEST iloczynem całek, a całka ilorazu funkcji NIE JEST ilorazem całek.
   
   

11. Sprawdź swoją wiedzę o całkach - zadania kontrolne

1. Ile wynosci

\[\int f'(x)\,dx=?\]

2. Czy następująca równość jest prawdziwa?

\[\int (2x^2+1)\,dx=2\int x^2\,dx+\int 1\,dx\]

3. Jakiej metody całkowania użyć do policzenia całki

\[\int \ln x\,dx=?\]

Zrób kolejny krok i ucz się całek na przykładach

• Następne »

Komentarzy (0)

• Imię
• E-mail (niewidoczny)
• Komentarz

WYŚLIJ