Oblicz macierz odwrotną do macierzy stopnia 2:
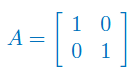
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Oblicz macierz odwrotną do macierzy stopnia 2:
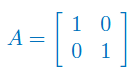
Oblicz macierz odwrotną do macierzy wymiaru 2x2:
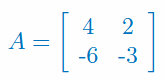
Oblicz dopełnienia algebraiczne wszystkich elementów macierzy:
\(\begin{bmatrix}0&-4\\1&2\end{bmatrix}\)
Oblicz macierz odwrotną przy użyciu metody Gaussa:
\(A=\begin{bmatrix}2&0\\3&1\end{bmatrix}\)
Czy istnieją macierze A i B, takie, że:
\(A\cdot B=I\,\,\textrm{ale}\,\,B\neq A^{-1}\)
Oblicz dopełnienia algebraiczne wszystkich elementów macierzy:
\(\begin{bmatrix}1&1&-2\\3&0&2\\-1&5&0\end{bmatrix}\)
Dla jakich wartości parametrów \(a,b,c,d\in\mathbb{R}\) istnieje macierz odwrotna do macierzy:
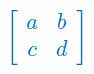
Korzystając z twierdzenia o macierzy odwrotnej oblicz macierz odwrotną do macierzy stopnia 3:
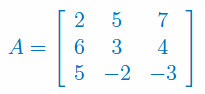
Korzystając z metody dołączonej macierzy jednostkowej (Gaussa) oblicz macierz odwrotną do macierzy:
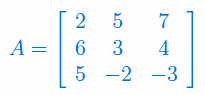
Oblicz macierz odwrotną do macierzy diagonalnej wymiaru 5x5:
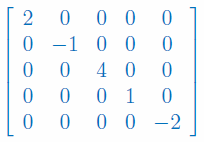
Oblicz macierz odwrotną do macierzy wymiaru 6x6:
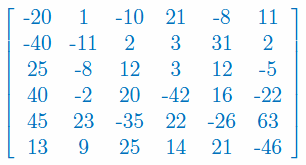
Oblicz macierz odwrotną metodą bezwyznacznikową:
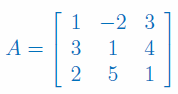
Oblicz macierz odwrotną do macierzy:
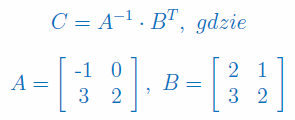
Używając metody bezwyznacznikowej wyznacz macierz odwrotną do macierzy:
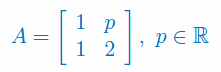
Oblicz macierz odwrotną do macierzy stopnia 4:
\(\begin{bmatrix}1&2&3&4\\2&3&1&2\\1&1&1&-1\\1&0&-2&-6\end{bmatrix}\)
Sprawdź czy macierz:
\(\begin{bmatrix}22&-6&-26&17\\-17&5&20&-13\\-1&0&2&-1\\4&-1&-5&3\end{bmatrix}\)
jest macierzą odwrotną do macierzy:
\(\begin{bmatrix}1&2&3&4\\2&3&1&2\\1&1&1&-1\\1&0&-2&-6\end{bmatrix}\)
Jesteś w kategorii Macierz odwrotna zadania z rozwiązaniami
Macierz odwrotna istnieje tylko dla macierzy kwadratowych i nieosobliwych (o wyznaczniku różnym od zera). Jest to taka macierz, że po pomnożeniu jej (prawo lub lewostronnie) przez macierz wyjściową otrzymamy macierz identycznościową (inaczej jednostkową, która ma jedynki na przekątnej i zera poza przekątną).
Istnieje kilka metod wyznaczania macierzy odwrotnych, z których najważniejsza jest metoda ze wzoru, w którym pojawia się wyznacznik macierzy, dopełnienia algebraiczne oraz transpozycja. Druga metoda to eliminacja Gaussa, gdzie obok macierzy wyjściowej dopisujemy macierz jednostkową i następnie za pomocą operacji elementarnych na wierszach przekształcamy macierzy po lewej stronie w macierz jednostkową. Macierz która powstanie po prawej stronie będzie macierzą odwrotną.