Start 
Rozwiąż równanie różniczkowe korzystając z transformaty Laplace'a:
\(ay'(x)+by(x)+c=0,\,\,a,b,c\in\mathbb{R}\)
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Równania różniczkowe I-go rzędu - zadania
Znaleźć całkę równania różniczkowego
\(y'=y\)
Rozwiąż równanie różniczkowe
\(y'=1\)
Znaleźć całkę równania różniczkowego
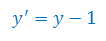
Rozwiązać równanie różniczkowe
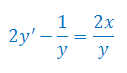
Rozwiązać równanie różniczkowe
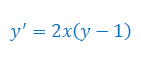
Rozwiązać równanie różniczkowe:
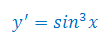
Rozwiązać równanie różniczkowe:
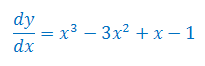
Rozwiązać równanie różniczkowe z warunkiem początkowym:
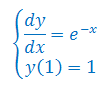
Rozwiązać równanie różniczkowe z warunkiem początkowym:
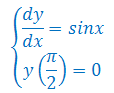
Scałkować podane równanie różniczkowe:
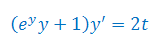
Scałkować podane równanie różniczkowe:
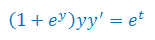
Scałkować podane równanie różniczkowe:
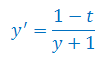
Rozwiązać równanie różniczkowe:
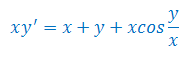
Rozwiązać równanie różniczkowe:
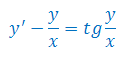
Rozwiązać równanie różniczkowe:
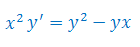
Rozwiązać równanie różniczkowe:
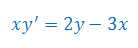
Rozwiązać równanie różniczkowe z warunkiem początkowym:
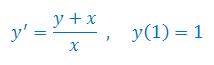
Rozwiązać równanie różniczkowe z warunkiem początkowym:
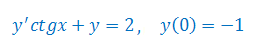
Scałkować podane równanie różniczkowe:
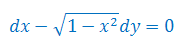
Rozwiązać równanie różniczkowe z warunkiem początkowym:
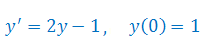
Rozwiązać równanie różniczkowe z warunkiem początkowym
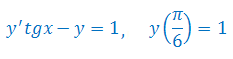
Rozwiązać równanie różniczkowe:
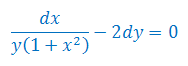
Rozwiązać równanie różniczkowe:
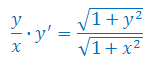
Rozwiązać równanie różniczkowe:
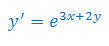
Rozwiązać równanie różniczkowe:
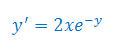
Rozwiązać równanie różniczkowe:
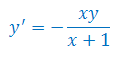
Rozwiązać równanie różniczkowe
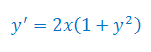
Rozwiązać równanie różniczkowe
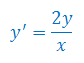
Znaleźć całkę równania różniczkowego
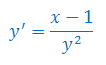
Rozwiąż równanie różniczkowe pierwszego rzędu
\(y'=\frac{1}{x^2+1}\)