Rozwiązać równanie różniczkowe

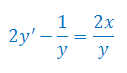
Rozwiązanie

Jak się okazuje, jest to równanie o rozdzielonych zmiennych, więc:

 Wskazówki

1. Przenosimy "wszystko" poza y' na jedną (prawą) stronę.
2. Zauważamy, że jest to równanie o rozdzielonych zmiennych, czyli równanie postaci
   \(y'=f(x)g(y)\), gdzie f(x) jest funkcją zmiennej x, a g(y) jest funkcją y.
   
3. Pamiętamy, że w równaniach różniczkowych zawsze \(y'=\frac{dy}{dx}\), tzn. że y jest funkcją x, więc pochodna y jest pochodną "po x-ie".
   
4. Przypominamy sobie, że równania o zmiennych rozdzielonych rozwiązuje się poprzez dzielenie obu stron równania przez funkcję g(y) i mnożenie przez dx, a następnie całkuje się obie strony, tzn.
   \(\frac{dy}{dx}=f(x)g(y)\)
   \(\frac{dy}{g(y)}=f(x)dx\)
   \(\int\frac{1}{g(y)}\,dy=\int f(x)\,dx\)
   
5. Jeśli to możliwe, zapisujemy ostateczny wynik w postaci y=h(x). W zadaniu jest to możliwe, rozwiązanie możemy zapisać w postaci
   \(y(x)=\sqrt{x^2+x+c}\), gdzie c jest dowolną stałą rzeczywistą

 UWAGA: Rozwiązanie równania różniczkowego I-go rzędu nazywa się całką równania, dlatego czasami treść tego typu zadań brzmi: "Scałkować podane równanie różniczkowe..." lub "Znaleźć całkę równania różniczkowego...".

• Następne »

Komentarzy (0)

• Imię
• E-mail (niewidoczny)
• Komentarz

WYŚLIJ