Start 
Zbadaj liczbę rozwiązań układu równań w zależności od parametru p:
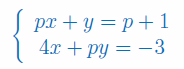
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Twierdzenie Kroneckera-Capellego - zadania i przykłady
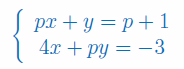
Zbadaj liczbę rozwiązań układu równań w zależności od parametru p:
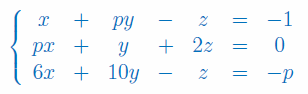
Dla jakich wartości parametru p układ równań ma tylko jedno rowiązanie:
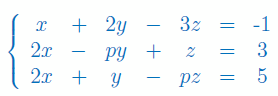
Stosując twierdzenie Kroneckera-Capellego zbadaj liczbę rozwiązań układu równań liniowych. Następnie rozwiąż układ (jeśli to konieczne przedstaw rozwiązania za pomocą parametrów):
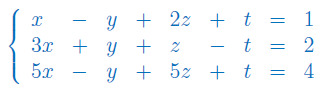
Określić liczbę rozwiązań układu równań przy użyciu twierdzenia Kroneckera-Capellego:
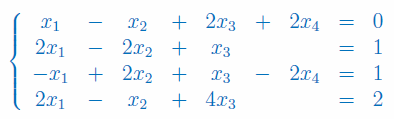
Jesteś w dziale Twierdzenie Kroneckera-Capellego zadania z rozwiązaniami
Twierdzenie Kroneckera-Capellego służy do określania liczby rozwiązań układów równań liniowych z dowolną liczbą niewiadomych i równań. Aby móc wyznaczyć liczbę rozwiązań układu równań należy obliczyć rząd macierzy głównej układu oraz rząd macierzy rozszerzonej. Układ posiada dokładnie jedno rozwiązanie, gdy rząd macierzy głównej jest równy rzędowi macierzy rozszerzonej i oba rzędy są równe niewiadomych w układzie. Układ ma natomiast nieskończenie wiele rozwiązań, gdy rzędy są równe, ale mniejsze niż liczba niewiadomych w układzie. Układ jest sprzeczny (nie posiada rozwiązań), gdy rząd macierzy głównej układu jest mniejszy od rzędu macierzy rozszerzonej.