Start 
Oblicz całkę krzywoliniową skierowaną daną równaniem funkcyjnym
\(\int\limits_L 2xy\, dx+ x^2 \,dy\)
gdzie L jest łukiem paraboli \(y(x)=x^2\) dla \(x\in[0,1]\).
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Całki krzywoliniowe - zadania z rozwiązaniami
Oblicz całkę krzywoliniową
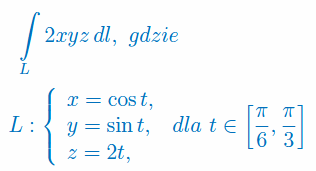
Oblicz całkę krzywoliniową
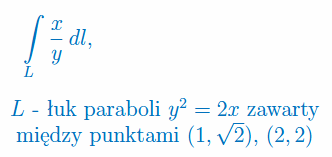
Oblicz długość łuku
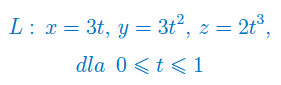
Oblicz całkę krzywoliniową skierowaną daną równaniem funkcyjnym
\(\int\limits_L xy\, dx-x^2 \,dy\)
gdzie L jest łukiem zadanym równaniem \(y(x)=\frac{1}{x}\) dla \(x\in[1,4]\).
Oblicz całkę krzywoliniową skierowaną daną równaniem funkcyjnym
\(\int\limits_L \frac{y}{x}\, dx+ \frac{x}{y} \,dy\)
gdzie L jest łukiem paraboli \(y(x)=x^2\) dla \(x\in[-1,1]\).
Oblicz całkę krzywoliniową skierowaną
\(\int\limits_L y\, dx+2x \,dy\)
gdzie L jest łukiem zadanym równaniem parametrycznym \(x=t-\sin t,\,y=1-\cos t\) dla \(t\in[0,2\pi]\).
Oblicz całkę krzywoliniową skierowaną
\(\int\limits_L x\, dx+y \,dy+z\,dz\)
gdzie L jest łukiem zadanym równaniem parametrycznym \(x=2t,\,y=t^2,\,z=1-t\) dla \(t\in[0,1]\).
Oblicz całkę krzywoliniową skierowaną
\(\int\limits_L dx+\,dy+\,dz\)
gdzie L jest łukiem zadanym równaniem parametrycznym \(x=t,\,y=t,\,z=t\) dla \(t\in[0,1]\).
Obliczyć długość łuku linii zadanej w postaci parametrycznej
\(x=3 \cos t,\,y=3\sin t,\,z=4t\) dla \(t\in[0,1]\).
Obliczyć długość łuku linii zadanej w postaci parametrycznej
\(x=t,\,y= t,\,z=t\) dla \(t\in[0,1]\).
Obliczyć masę jednorodnego półokręgu
\(L:x^2+y^2=R^2,\,\,y\ge 0,\,\,\rho=C=const\).
Obliczyć momenty statyczne jednorodnego półokręgu
\(L:x^2+y^2=R^2,\,\,y\ge 0,\,\,\rho=C=const\).
Obliczyć współrzędne środka masy jednorodnego półokręgu
\(L:x^2+y^2=R^2,\,\,y\ge 0,\,\,\rho=C=const\).