Start 
Oblicz drugą pochodną funkcji:
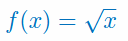
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Pochodne wyższych rzędów - zadania z rozwiązaniami
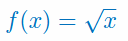
Oblicz trzecią pochodną funkcji:
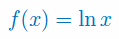
Oblicz pochodne \(f',\,f'',\,f'''\) dla funkcji:
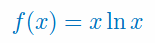
Wiedząc, że funkcja f ma trzy pierwsze pochodne, oblicz pochodne \(y',\,y'',\,y'''\) dla funkcji:
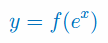
Znajdź wszystkie rozwiązania równania:
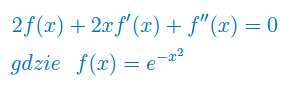
Oblicz pochodne rzędu 1,2,3,4 i 5 dla funkcji:
\(f(x)=\frac{1}{x}\)
Następnie podaj ogólny wzór na pochodną n-tego rzędu (\(n\in\mathbb{N}\)).
Oblicz pochodne rzędu 1,2,3,4 i 5 dla funkcji:
\(f(x)=\sin x\)
Następnie podaj ogólny wzór na pochodną n-tego rzędu (\(n\in\mathbb{N}\)).
Oblicz pochodne rzędu 1,2,3,4 i 5 dla funkcji:
\(f(x)=\cos x\)
Następnie podaj ogólny wzór na pochodną n-tego rzędu (\(n\in\mathbb{N}\)).
Oblicz pochodne rzędu 1,2,3,4 i 5 dla funkcji:
\(f(x)=2^x\)
Następnie podaj ogólny wzór na pochodną n-tego rzędu (\(n\in\mathbb{N}\)).
Oblicz n-tą pochodną wielomianu stopnia n (\(n\in\mathbb{N},\,\,a_1,a_2,...,a_n\in\mathbb{R}\)):
\(W(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\)
Ile wynosi pochodna rzędu \(n+k\), gdzie \(k=1,2,3,...\).