Rozwiąż układ równań liniowych z 2 niewiadomymi:
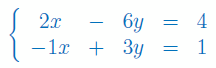
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Rozwiąż układ równań liniowych z 2 niewiadomymi:
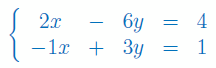
Rozwiąż układ Cramera z 2 niewiadomymi:
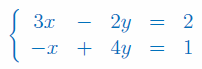
Stosując wzory Cramera wyznacz niewiadomą y
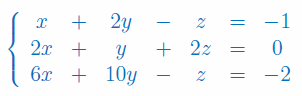
Zbadać dla jakich wartości parametru p układ równań jest układem Cramera. Następnnie wyznaczyć wartości niewiadomych
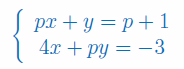
Rozwiązać układ równań metodą wyznacznikową:
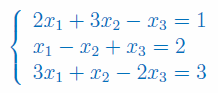
Inwestor chce kupić akcje za 100 tys. zł, chcąc uzyskać przeciętny (średni) zysk w ciagu pół roku na poziomie 13,5%, przy ryzyku w wysokości 10%. Doradca inwestycyjny oferuje mu 3 pakiety akcji o róznym średnim wzroście i ryzyku:
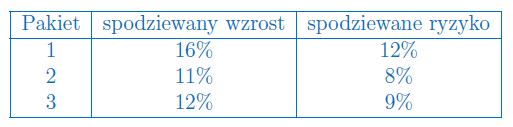
Jakie kwoty pieniędzy powinien zainwestować inwestor w akcjie z każdego pakietu, żeby zrealizować swój cel inwestycyjny?
Rozwiąż układ Cramera z 3 niewiadomymi:
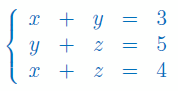
Zbadaj liczbę rozwiązań układu równań w zależności od parametru p. Dla p=2, korzystając ze wzorów Cramera wyznacz wartość niewiadomej y:
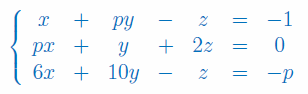
Rozwiąż układ równań z 2 niewiadomymi (x,y) metodą przeciwnych współczynników oraz za pomocą wzorów Cramera:
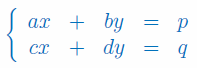
gdzie \(a,b,c,d,p,q\in\mathbb{R}\).
Dla jakich wartości parametru p układ równań jest układem Cramera:
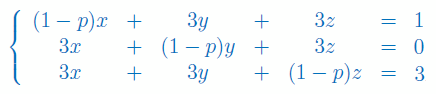
Rozwiąż układ równań stosując wzory Cramera
\(\left\{\begin{array}{ccccccccccc}x_1&+&x_2&+&x_3&+&x_4&+&x_5&=&5\\2x_1&+&x_2&-&x_3&+&3x_4&+&x_5&=&6\\5x_1&-&2x_2&+&x_3&+&x_4&-&x_5&=&4\\-x_1&+&x_2&+&3x_3&+&2x_4&+&2x_5&=&7\\x_1&-&x_2&+&x_3&-&x_4&+&x_5&=&1\end{array}\right.\)
Rozwiąż układ równań stosując wzory Cramera
\(\left\{\begin{array}{ccccccccc}x_1&+&x_2&+&x_3&+&x_4&=&4\\2x_1&+&x_2&-&x_3&+&3x_4&=&5\\5x_1&-&2x_2&+&x_3&+&x_4&=&5\\-x_1&+&x_2&+&3x_3&+&2x_4&=&5\end{array}\right.\)
Rozwiąż układ równań stosując wzory Cramera
\(\left\{\begin{array}{ccccccc}x&+&y&+&z&=&5\\2x&+&2y&+&z&=&3\\3x&+&2y&+&z&=&1\end{array}\right.\)
Rozwiąż układ równań metodą eliminacji Gaussa:
\(\left\{\begin{array}{ccccccc}x&+&2y&+&3z&=&4\\&& y& +&2z&=&3\\&&&&4z&=&4\end{array}\right.\)
Rozwiązać układ równań przy użyciu metody eliminacji Gaussa:
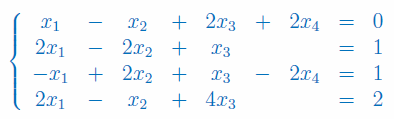
Rozwiązać układ równań metodą eliminacji Gaussa:
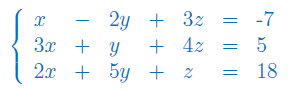
Rozwiąż metodą eliminacji Gaussa:
\(\left\{\begin{array}{ccccccccc}2x_1&+&x_2&-&x_3&+&x_4&=&1\\&& x_2& +&3x_3&-&3x_4&=&1\\x_1&+&x_2&+&x_3&-&x_4&=&1\end{array}\right.\)
Rozwiąż układ metodą eliminacji Gaussa:
\(\left\{\begin{array}{ccccccccc}2x_1&+&x_2&-&x_3&+&x_4&=&1\\3x_1&-&2x_2&+&2x_3&-&3x_4&=&2\\5x_1&+&x_2&-&x_3&+&2x_4&=&-1\\2x_1&-&x_2&+&x_3&-&3x_4&=&4\end{array}\right.\)
Rozwiąż układ metodą eliminacji Gaussa:
\(\left\{\begin{array}{ccccccc}2x_1&+&x_2&+&x_3&=&1\\3x_1&-&x_2&+&3x_3&=&2\\x_1&+&x_2&+&x_3&=&0\\x_1&-&x_2&+&x_3&=&1\end{array}\right.\)
Zbadaj liczbę rozwiązań układu równań w zależności od parametru p:
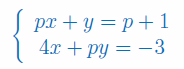
Stosując twierdzenie Kroneckera-Capellego zbadaj liczbę rozwiązań układu równań liniowych. Następnie rozwiąż układ (jeśli to konieczne przedstaw rozwiązania za pomocą parametrów):
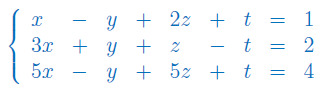
Określić liczbę rozwiązań układu równań przy użyciu twierdzenia Kroneckera-Capellego:
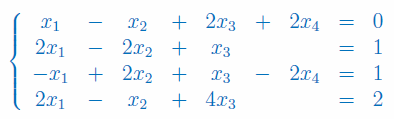
Dla jakich wartości parametru p układ równań ma tylko jedno rowiązanie:
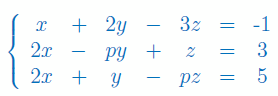
Zbadaj liczbę rozwiązań układu równań w zależności od parametru p:
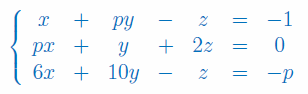
Zapisz macierz główną układu równań:
\(\left\{\begin{array}{ccccccc}x&-&4y&+&5z&=&2\\&& 2y& -&z&=&1\\4x&+& 2y&+&z&=&0\end{array}\right.\)
Podać przykład sprzecznego układu równań liniowych
Zapisz układ równań w postaci macierzowej:
\(\left\{\begin{array}{cccccccccc}2x&+&y&-&z&+&3t&=&1\\-x&+&7y&-&3z&-&5t&=&2\\2x&&&+&9z&-&2t&=&3\\x&+&y&&&+&2t&=&4\end{array}\right.\)
Rozwiązując odpowiedni układ równań, wyznacz równanie trójmianu kwadratowego przechodzącego przez punkty:
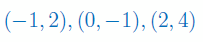
Rozwiąż układ równań z 3 niewiadomymi metodą macierzową:
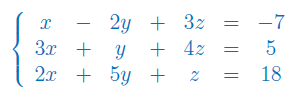
Jesteś w dziale Układy równań liniowych zadania z rozwiązaniami
W tej kategorii znajdziesz rozwiązania typowych zadań z zakresu układów równań liniowych, w tym przykłady rozwiązywania układów Cramera, metody eliminacji Gaussa, twierdzenia Kroneckera-Capellego oraz przykłady pokazujące inne metody rozwiązywania układów równań.
Układy równań liniowych są ściśle związane z macierzami i wyznacznikami, ponieważ niemal w każdej metodzie rozwiązywania układów stosujemy pojęcia związane z macierzami, np. układy Cramera rozwiązujemy za pomocą wzorów Cramera, w których występują wyznaczniki.
Metoda eliminacji Gaussa polega na zapisaniu układu w postaci macierzowej i przeprowadzanie operacji elementarnych na wierszach macierzy rozszerzonej tak długo, aż otrzymamy macierz schodkową. Naszym celem w tej metodzie jest więc zerowanie elementów.
Twierdzenie Kroneckera-Capellego służy do wyznaczania liczby rozwiązań układu równań liniowych i wykorzystuje pojęcie rzędu macierzy. Do innych metod rozwiązywania układów równań możemy zaliczyć metody znane ze szkoły średniej: metoda podstawaiania, graficzna czy metoda przeciwnych współczynników (metody te sprawdzają się jedynie w przypadku układów o małej liczbie równań i niewiadomych - w praktyce 2 równań z 2 niewiadomymi).
Aby uzyskać możliwie najlepsze efekty nauki, warto przeanalizować rozwiązania jak największej loczby zadań z układów równań, następnie trzeba rozwiązać jak najwięcej zadań samodzielnie. Tylko tak można opanować materiał na tyle dobrze by poradzić sobie na kolokwium lub egzaminie. Często będzie Ci się wydawało, że wystarczy zobaczyć rozwiązanie i je zrozumieć - nic bardziej mylnego. Aby naprawdę nauczyć się rozwiązywać zadania skutecznie i bezbłednie, należy rozwiązywać zadania samodzielnie. Jeśli coś w rozwiązaniu zadania będzie niejasne to możesz zadać pytanie w komentarzu pod zadaniem. Na tej stronie obowiązuje zasada, że nie ma głupich pytań i na każde pytanie uzyskasz odpowiedź.