Rozwiąż układ równań liniowych z 2 niewiadomymi
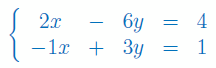
Rozwiązanie

Zatem nasz układ równań nie jest układem Cramera (nie ma jednego rozwiązania) i do jego rozwiązania nie można zastosować wzorów Cramera.
Możliwe są 2 przypadki, albo układ jest sprzeczny (nie ma rozwiązań), albo ma nieskończenie wiele rozwiązań.
Zauważmy, że, gdy pomnożymy drugie równanie przez -2, to otrzymamy następujący układ równań (równoważny wyjściowemu):
\[\left\{\begin{array}{c}2x-6y=4\\2x-6y=-2\end{array}\right.\]
Układ ten jest sprzeczny, ponieważ gdy odejmiemy równania stronami, to otrzymamy sprzeczność 0=6.
Zatem nasz wyjściowy układ równań też jest sprzeczny (nie posiada rozwiązań).
UWAGA
Układ nie jest układem Cramera, ponieważ macierz główna układu (ozn. A) jest osobliwa (ma wyznacznik równy 0).

Komentarzy (2)