Oblicz moduł i argument liczby zespolonej oraz zaznacz je na płaszczyźnie zespolonej
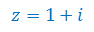
Rozwiązanie

Rysunek

Wskazówki
Moduł liczby zespolonej \(z=x+yi\), liczymy ze wzoru
\(|z|=\sqrt{x^2+y^2}\)
Moduł liczby zespolonej z interpretuje się jako odległość tej liczby od początku układu współrzędnych.
Argument główny liczby zespolonej \(z\)
to kąt między dodatnią częścią osi rzeczywistej (\(Re(z)\)), a promieniem wodzącym liczby zespolonej \(z\).
Zwykle zakłada się, że \(0\le \arg(z)<2\pi\), ale możesz spotkać się też z warunkiem \(-\pi<\arg(z)\le \pi\). Oba warunki są równoważne.
Niech \(z=x+yi\) oraz \(\arg(z)=\varphi\), wtedy
\(\sin \varphi=\frac{y}{|z|}\)
\(\cos \varphi=\frac{x}{|z|}\)
co więcej \(\arg(0)=0\).
Metody wyznaczania argumentu głównego
- metoda graficzna - zaznaczamy liczbę zespoloną na płaszczyźnie zespolonej (liczbie \(z=x+yi\) odpowiada punkt o współrzędnych (x,y)) i "na oko" wyznaczamy kąt jaki jest utworzony między dodatnią częścią osi rzeczywistej, a promieniem wodzącym liczby zespolonej
- z układu równań (\(z=x+yi\) - dane, \(\varphi\) - szukane):
\[\sin \varphi=\frac{y}{|z|},\,\,\,\cos \varphi=\frac{x}{|z|}\] - z arcusa tangensa (tylko, gdy \(x>0,\,y>0\)):
\[\arg(z)=arctg\left(\frac{y}{x}\right),\,\,x>0,\,\,y>0\]
Zwykle stosuje się metodę graficzną (to podstawa!) plus jedna z metod 2 lub 3.
Szybki sposób wyznaczania argumentu:
1 określ, w której ćwiartce płaszczyzny zespolonej leży argument (aby to zrobić wystarczy zaznaczyć liczbę zespoloną na płaszczyźnie i zobaczyć w której ćwiartce się znajduje)
2. wyznacz wartość takiego kąta \(\varphi\) leżącego w ćwiartce wyznaczonej w pkt 1, którego sinus jest równy \(\frac{y}{|z|}\) lub cosinus jest równy \(\frac{x}{|z|}\). Wystarczy obliczyć tylko wartość sinusa lub tylko wartość cosinusa, nie trzeba liczyć obu.
Niech \(z=x+yi\), gdzie \(x,y\in\mathbb{R}\).
Gdy liczba zespolona \(z\) leży w I ćwiartce płaszczyzny zespolonej (\(x\ge 0,y\ge 0\)), to: \[0\le \arg(z)\le \frac{\pi}{2}\]
Gdy liczba zespolona \(z\) leży w II ćwiartce płaszczyzny zespolonej (\(x\le 0,y\ge 0\)), to: \[\frac{\pi}{2}\le \arg(z)\le \pi\]
Gdy liczba zespolona \(z\) leży w III ćwiartce płaszczyzny zespolonej (\(x\le 0,y\le 0\)), to: \[\pi\le \arg(z)\le \frac{3}{2}\pi\]
Gdy liczba zespolona \(z\) leży w IV ćwiartce płaszczyzny zespolonej (\(x\ge 0,y\ge 0\)), to: \[\frac{3}{2}\pi\le \arg(z)\le 2\pi\]
Bardzo ważna w tego typu zadaniach jest znajomość funkcji trygonometrycznych, szczególnie wartości sinusa i cosinusa podstawowych kątów (warto nauczyć się na pamięć!):


Komentarzy (0)