Korzystając z Tw. Weierstrassa uzasadnij zbieżność bezwzględną i jednostajną szeregu funkcyjnego

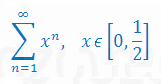
Rozwiązanie

Wskazówki:

1. \(x\in\left[0,\frac{1}{2}\right]\), więc \(x\le\frac{1}{2}\), a stąd wynika, że \(|x|^n\le\left(\frac{1}{2}\right)^n\)
2. Liczymy granicę \(\lim\limits_{n\to\infty} \sqrt[n]{a_n}\), która wynosi \(\frac{1}{2}\).
   Zatem na mocy kryterium Cauchy'ego szereg liczbowy jest zbieżny.
3. Twierdzenie Weierstrassa o zbieżności jednostajnej szeregu funkcyjnego:
   Jeżeli \(|f_n(x)|\le a_n\) dla \(x\in X\) i szereg liczbowy \(\sum\limits_{n=1}^\infty a_n\) jest zbieżny, to szereg funkcyjny \(\sum\limits_{n=1}^\infty f_n(x)\) jest zbieżny jednostajnie i bezwzględnie dla \(x\in X\).

• « Poprzednie

Komentarzy (0)

• Imię
• E-mail (niewidoczny)
• Komentarz

WYŚLIJ