Określ dziedzinę funkcji
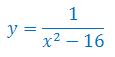
Rozwiązanie
Aby wyznaczyć dziedzinę funkcji, sprawdzamy dla jakich "x" mianownik jest różny od zera:

Na koniec wykres funkcji \(y=\frac{1}{x^2-16}\), na którym widać,
że punkty \(x=-4\) i \(x=4\) nie należą do dziedziny (w tych punktach są asymptoty pionowe):
Wskazówki
W przykładzie sprawdzamy dla jakich \(x\) zeruje się mianownik naszej funkcji, czyli \(x^2-16\neq 0\).
Liczby dla których mianownik jest równy zero odrzucamy, ponieważ nie można dziecić przez zero.
Co to jest dziedzina funkcji?
Dziedzina funkcji jest to zbiór takich x, dla których istnieją wartości funkcji (czyli są to wszystkie x, które można podstawić do wzoru funkcji).
Innymi słowy dziedzina jest zbiorem wszystkich argumentów funkcji.
Na co zwrócić uwagę przy wyznaczaniu dziedziny?
Oczywiście zwracaj zawsze uwagę na działania niedozwolone w matematyce:
- dzielenie przez 0, np.\[f(x)=\frac{g(x)}{h(x)},\,\,\textrm{wtedy}\,\,h(x)\neq 0\]
- pierwiastkowanie (stopnia parzystego) liczb ujemnych, np.\[f(x)=\sqrt{g(x)},\,\,\textrm{wtedy}\,\,g(x)\ge 0\]
- logarytmowanie liczb ujemnych, np.\[f(x)=\ln(g(x)),\,\,\textrm{wtedy}\,\,g(x)>0\]

Komentarzy (1)