Oblicz wyznacznik macierzy 3x3
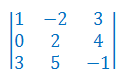
Rozwiązanie
Stosujemy rozwinięcie Laplace'a względem pierwszej kolumny:

UWAGA: Wyznaczniki macierzy stopnia 3 można obliczyć za pomocą rozwinięcia Laplace'a oraz stosując regułę Sarrusa. Zobacz koniecznie przewodnik zawierający omówienie różnych metod obliczania wyznaczników macierzy.
Wskazówki
Rozwinięcie Laplace'a jest uniwersalną metodą liczenia wyznacznika macierzy. Za pomocą metody Laplace'a możemy obliczyć wyznacznik macierzy dowolnego stopnia (zobacz przykład jak obliczyć wyznacznik macierzy 4x4).
Rozwinięcie Laplace'a stosuje się względem wybranego wiersza lub kolumny. Wybierając wiersz lub kolumnę z największą liczbą zer możemy uprościć nasze obliczenia.
W przypadku macierzy A stopnia n, schemat metody Laplace'a wygląda następująco:
1. Wybieramy wiersz lub kolumnę macierzy, w której znajduje się najwięcej zer
2. "Rozwijamy" wyznacznik względem wybranego wiersza lub kolumny wyliczając wyznaczniki macierzy stopni n-1 (dopełnienia algebraiczne kolejnych elementów).
W przypadku rozwinięcia względem i-tego wiersza (gdzie \(i=1,2,\ldots,n\)) schemat metody Laplace'a wygląda następująco:
\[\det A=a_{i1}\cdot (-1)^{i+1}\cdot\det A_{i1}+a_{i2}\cdot (-1)^{i+2}\cdot\det A_{i2}+\ldots +a_{in}\cdot (-1)^{i+j} \cdot\det A_{in}=\]\[=\sum\limits_{k=1}^n a_{ik}\cdot (-1)^{i+k}\cdot \det A_{ik}\]
gdzie \(A_{ij}\) jest macierzą stopnia n-1 otrzymaną z macierzy A przez skreślenie i-tego wiersza i j-tej kolumny (\(\det A_{ij}\) to minor macierzy), np. \(A_{12}\) to macierz powstała przez usunięcie 1-go wiersza i 2-giej kolumny w macierzy A.
Zauważ, że \((-1)^{i+k}\) będzie na przemian równe -1 i 1 lub 1 i -1, więc w rozwinięciu Laplace'a kolejne wyrażenia mają na przemian znak minus i plus (lub plus i minus).
W przypadku rozwinięcia względem j-tej kolumny (gdzie \(j=1,2,\ldots,n\)) mamy następujący wzór na wyznacznik:
\[\det A=a_{1j}\cdot (-1)^{1+j}\cdot \det A_{1j}+a_{2j}\cdot (-1)^{2+j}\cdot \det A_{2j}+\ldots +a_{nj}\cdot (-1)^{n+j}\cdot\det A_{nj}=\]\[=\sum\limits_{k=1}^n a_{kj}\cdot (-1)^{k+j}\cdot\det A_{kj}\]
np. gdy \(j=1\) to rozwinięcie Laplace'a następuje względem pierwszej kolumny:
\[\det A=a_{11}\cdot (-1)^{1+1}\cdot\det A_{11}+a_{21}\cdot (-1)^{2+1}\cdot\det A_{21}+\ldots +a_{n1}\cdot (-1)^{n+1}\cdot\det A_{n1}=\]\[=a_{11}\cdot\det A_{11}-a_{21}\cdot\det A_{21}+\ldots +a_{n1}\cdot (-1)^{n+1}\cdot\det A_{n1}\]
Używając dopełnień algebraicznych rozwinięcie Laplace'a względem i-tego wiersza można zapisać następująco:
\[\det A=a_{i1}\cdot D_{i1}+a_{i2}\cdot D_{i2}+\ldots +a_{in}\cdot D_{in}=\sum\limits_{k=1}^n a_{ik}\cdot D_{ik}\]
Natomiast rozwinięcie względem j-tej kolumny wygląda tak:
\[\det A=a_{1j}\cdot D_{1j}+a_{2j}\cdot D_{2j}+\ldots +a_{nj}\cdot D_{nj}=\sum\limits_{k=1}^n a_{kj}\cdot D_{kj}\]

Komentarzy (0)