NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!

Oblicz całkę nieoznaczoną

Całka z tgh x

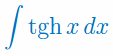
Rozwiązanie

Całka wynosi

Całka z tgh x - wzór

ponieważ

całka z tghx

\(tgh{x}=\frac{\sinh x}{\cosh x}\)
Stosujemy całkowanie przez podstawienie. Przypominamy sobie wzór na pochodną cosinusa hiperbolicznego \((\cosh x)'=\sinh x\)
Po podstawieniu \(\frac{\sinh x}{\cosh x}\,dx=\frac{1}{u}\,du\)
Stosujemy podstawowy wzór na całkę z \(u^{-1}\)
Wracamy do zmiennej x, bo \(u=\cosh x\)

- Odpowiedz
sebo! 8 lat temu
@ZjemCiMaslo W tym zadaniu liczymy całkę z funkcji hiperbolicznej \(tgh x\), a nie trygonometrycznej \(tg x\), więc rozwiązanie jest jak najbardziej poprawne. Tutaj znajdzie Pan rozwiązanie całki z funkcji trygonometrycznej \(tg x\).
- Odpowiedz
ZjemCiMaslo 8 lat temu
Witam,
Ze wzorów na pochodne wychodzi że \(\cos' x=-\sin x\), dlatego całka z \(tg x\) wynosi \(-\ln(\cos x)+C\)