Oblicz całkę nieoznaczoną

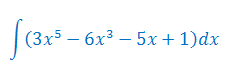
Rozwiązanie

Całka wynosi

\[\int (3x^5-6x^3-5x+1)\,dx=3\cdot \frac{x^6}{6}-6\cdot \frac{x^4}{4}-5\cdot \frac{x^2}{2}+x+c=\frac{x^6}{2}-\frac{3}{2}x^4-\frac{5}{2}x^2+x+c\]

Wskazówki

1. Korzystamy z własności całki nieoznaczonej (całka sumy funkcji jest sumą całek każdej funkcji z osobna, stałe można wyciągać przed całkę)
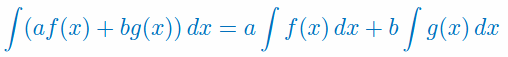
   stąd
   \(\int (3x^5-6x^3-5x+1)\,dx=3\int x^5\,dx-6\int x^3\,dx-5\int x\,dx+\int 1\,dx\)
   
   
2. Korzystamy z podstawowego wzoru na całkę funkcji potęgowej:
       
   stąd, np. \(\int 1\,dx=\int x^0\,dx=x+c\)

• « Poprzednie
• Następne »

Komentarzy (2)

• Imię
• E-mail (niewidoczny)
• Komentarz

WYŚLIJ

• 

  • Odpowiedz

  sebo! 5 lat temu

  @EwaZiniewicz Prawie dobrze, powinno być \(-\frac{3}{2}x^4\)
• 

  • Odpowiedz

  EwaZiniewicz 5 lat temu

  jeżeli wynik u mnie wynosi = \(1/2 x^6 + 3/2 x^4 - 5/2 x^2 + x + c\), to jest prawidlowy ?