Podaj wzór na całkę nieoznaczoną z funkcji \(\frac{1}{\sin^2x}\)

Całka z 1 przez sin kwadrat x

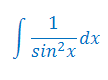
Rozwiązanie

Całka wynosi

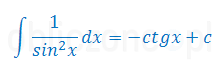
gdzie \(ctg x\) to funkcja trygonometryczna cotangens

\[ctg x=\frac{\cos x}{\sin x}\]

Wyjaśnienie

Całkowanie funkcji jest operacją odwrotną do różniczkowania funkcji (liczenia pochodnej), zatem wzór na całkę \(\int \frac{1}{\sin^2x}dx\) wynika z faktu, że pochodna funkcji \(ctg x\) wynosi \(-\frac{1}{\sin^2 x}\):

\[(-ctg{x}+c)'=-(ctg{x})'+(c)'=\frac{1}{\sin^2{x}}+0=\frac{1}{\sin^2{x}}\]

Wzór na całkę z \(\frac{1}{\sin^2x}\) należy zapamiętać. Najłatwiej to zrobić, gdy zna się wzory na pochodne funkcji elementarnych.

Komentarzy (3)

- Odpowiedz
Amadeusz 5 lat temu
@sebo! Dziękuję bardzo, jest PAN NAJLEPSZY!!! Ratuje mi Pan mój studencki kuperek :). Pozdrawiam cieplutko!!!!
- Odpowiedz
sebo! 5 lat temu
@Amadeusz Chodzi o całkę? \[\int \frac{\sin2x}{\sin^2 x-3\sin x+2}dx\] Trzeba zastosować tu wzór na sinus podwojonego kąta, czyli \(\sin 2x=2\sin x \cos x\), następnie całkowanie przez podstawienie, gdzie należy zastosować podstawienie \(\sin x=t\), wtedy \((\sin x)'dx=dt\) i stąd \(\cos xdx=dt\). Stosując to podstawienie dostaniemy całkę \[\int \frac{2t dt}{t^2-3t+2}\] którą już dużo łatwiej policzyć. Wystarczy zapisać ją trochę inaczej \[\int \frac{(2t-3+3)dt}{t^2-3t+2}=\int \frac{(2t-3)dt}{t^2-3t+2}+\int \frac{3dt}{t^2-3t+2}\] Pierwszą z tych całek liczymy stosując podstawienie \(t^2=u\), w drugiej trzeba zastosować przejście na postać kanoniczną dwumianu i podstawienie prowadzące do całki funkcji cyklometrycznej.
- Odpowiedz
Amadeusz 5 lat temu
Mam pytanie, na egzaminie dostałem całke z sin2x/(sin^2x-3sinx+2) i nie mam bladego pojęcia jak się do tego zabrać mógłby Pan dać wskazówke, czy robic przez czesci czy przez podstawianie( a jesli tak to jakie). Pozdrawiam