Oblicz rząd macierzy

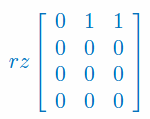
Rozwiązanie

Wskazówki

Równoważne definicje rzędu macierzy:

1. Rząd macierzy jest równy liczbie schodków w macierzy schodkowej (do postaci schodkowej można doprowadzić macierz poprzez wykonywanie operacji elementarnych na wierszach i kolumnach)
2. Rząd macierzy jest równy maksymalnemu stopniowi niezerowego minora macierzy (minor to wyznacznik macierzy powstałej przez skreślanie wierszy i/lub kolumn macierzy)
3. Rząd macierzy jest równy maksymalnej liczbie liniowo niezależnych wektorów tworzących wiersze (kolumny) macierzy
   
   

Własności rzędu macierzy:

1. Jeżeli A jest macierzą wymiaru \(n\times m\), to \(0 \le rzA\le\min\{n,m\}\)
2. \(rzA=0\Leftrightarrow A=0\)
3. Operacje elementarne na wierszach i/lub kolumnach nie zmieniają rzędu macierzy
   
   

Operacje elementarne, które nie zmieniają rzędu macierzy:

1. zamiana wierszy (kolumn) między sobą (\(w_{i}\leftrightarrow w_{j}\));
2. dodanie do elementów dowolnego wiersza (kolumny) odpowiadających im elementów innego wiersza (kolumny) pomnożonego przez dowolną liczbę (\(w_{i}+c\cdot w_{j}\));
3. mnożenie całego wiersza (kolumny) przez dowolną liczbę różną od zera (\(c\cdot w_{i}\)).  

• « Poprzednie
• Następne »

Komentarzy (0)

• Imię
• E-mail (niewidoczny)
• Komentarz

WYŚLIJ