Oblicz granicę niewłaściwą funkcji
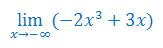
Rozwiązanie
Sprawdzamy najpierw "do czego" dąży każda z funkcji w naszej granicy. Próbujemy skorzystać z twierdzeń o arytmetyce granic niewłaściwych, ale nie możemy tego zrobić, ponieważ otrzymujemy symbol nieoznaczony \([\infty-\infty]\).
Wyciągniemy więc przed nawias \(x\) w najwyższej potędze i znowu sprawdzamy "do czego" dążą funkcje. Tym razem uda nam się zastosować twierdzenie o arytmetyce granic niewłaściwych:

Wskazówki
1. Otrzymujemy symbol nieoznaczony \([\infty-\infty]\), musimy więc przekształcić nasze wyrażenie wyciągając \(x^3\) przed nawias (czyli \(x\) podniesiony do najwyższej potęgi występującej w naszym wyrażeniu):
\[-2x^3+3x=x^3\left(-2+\frac{3}{x^2}\right)\]
2. Korzystamy z faktu, że granica niewłaściwa typu \(\frac{g}{\infty}\), gdzie \(g\) jest dowolną liczbą rzeczywistą, jest równa 0, czyli:
\[\lim\limits_{x\to-\infty}\frac{3}{x^2}=\left[\frac{3}{\infty}\right]=0\]
3. W ten sposób otrzymujemy wyrażenie typu \([-\infty\cdot (-2)]\), co daje \(\infty\)
UWAGA: Błędem jest przyjęcie, że \([\infty-\infty]=0\) i zastosowanie tego "chwytu" przy liczeniu naszej granicy (nie można tego zrobić!):
\[\lim\limits_{x\to-\infty}(-2x^3+3x)=[\infty-\infty]=0\,\,-\,\textrm{źle!!!}\]
Zobacz koniecznie najczęstsze błędy przy liczeniu granic funkcji.
Jak radzić sobie z granicami niewłaściwymi?
Poniżej znajdziesz zestawienie najważniejszych zasad liczenia granic niewłaściwych, często nazywa się to arytmetyką granic niewłaściwych (lub nawet twierdzeniem o arytmetyce granic niewłaściwych):
Granica z wyrażenia: liczba + "nieskończoność" = "nieskończoność"
\(g+\infty=\infty+g=\infty,\,\,gdy\,\,-\infty<g\le \infty\)
Granica z wyrażenia: liczba razy "nieskończoność" = "nieskończoność"
\(g\cdot\infty=\infty\cdot g=\infty,\,\,gdy\,\,0<g\le \infty\)
Granica z wyrażenia: liczba dzielona przez "nieskończoność" = 0
\(\frac{g}{\infty}=0,\,\,gdy\,\,-\infty<g<\infty\)
Granica z wyrażenia: liczba dzielona przez 0 = "nieskończoność"
\(\frac{g}{0^+}=\infty,\,\,gdy\,\,0<g<\infty\)
Granica z wyrażenia: liczba do potęgi "nieskończoność" = 0, gdy liczba jest dodatnia i mniejsza od 1
\(g^{\infty}=0,\,\,gdy\,\,0<g<1\)
Granica z wyrażenia: liczba do potęgi "nieskończoność" = "nieskończoność", gdy liczba jest większa od 1
\(g^{\infty}=\infty,\,\,gdy\,\,1<g\le \infty\)
Granica z wyrażenia: "nieskończoność" do potęgi liczba = 0, gdy liczba jest ujemna
\(\infty^{g}=0,\,\,gdy\,\,-\infty<g< 0\)
Granica z wyrażenia: "nieskończoność" do potęgi liczba = "nieskończoność", gdy liczba jest dodatnia
\(\infty^{g}=\infty,\,\,gdy\,\,0<g\le \infty\)
Jak pozbyć się symbolu nieoznaczonego?
W wielu zadaniach nie można bezpośrednio obliczyć granicy, ponieważ pojawiają się symbole nieoznaczone typu:
\[\left[\frac{0}{0}\right],\,\,\,\left[\frac{\infty}{\infty}\right],\,\,\,[\infty-\infty],\,\,\,[0\cdot \infty],\,\,\,\left[1^{\infty}\right],\,\,\,\left[\infty^{0}\right],\,\,\,\left[0^{0}\right]\]
Zapamiętaj, że wyrażenia nieoznaczone nie mają znaczenia liczbowego, bo np, nie można dzielić przez 0, a nieskończoność to nawet nie liczba tylko obiekt.
Wartości tych wyrażeń są różne w przypadku różnych funkcji.
Bardzo często wystarczy wykonać proste przekształcenie, dzięki któremu można łatwo pozbyć się symbolu nieoznaczonego:
1. Spróbuj wyciągnąć x do najwyższej potęgi przed nawias (jeśli liczysz granicę z funkcji wymiernej, to wyciągnij najwyższą potęgę w liczniku i mianowniku i skróć co się da).
2. Jeśli liczysz granicę z funkcji wymiernej, to zastosuj rozkład na czynniki lub zastosuj wzór skróconego mnożenia w liczniku i mianowniku, następnie skróć co się da.
Jak przekształcać symbole nieoznaczone, aby uzyskać \(\frac{0}{0}\) lub \(\frac{\infty}{\infty}\)?
Jeśli chcesz zastosować regułę de L'Hospitala, to musisz przekształcić symbol nieoznaczony do postaci:
\[\frac{0}{0}\,\,\,\textrm{lub}\,\,\,\frac{\infty}{\infty}\]
ponieważ tylko dla takich symboli "działa" reguła de L'Hospitala. Oto najczęściej stosowane przekształcenia:
1. Gdy \(f\cdot g\to\left[0\cdot \infty\right]\), to możemy zastosować tożsamość \(f\cdot g=\frac{f}{\frac{1}{g}}\) otrzymując symbol nieoznaczony \(\frac{0}{0}\) lub \(\frac{\infty}{\infty}\).
2. Gdy \(\frac{1}{f}\pm \frac{1}{g}\to\left[\infty- \infty\right]\), to możemy zastosować tożsamość \(\frac{1}{f}\pm \frac{1}{g}=\frac{g\pm f}{f\cdot g}\) otrzymując symbol nieoznaczony \(\frac{0}{0}\)
3. Gdy \(f-g\to\left[\infty- \infty\right]\), to możemy zastosować tożsamość \(f-g=\frac{\frac{1}{g}-\frac{1}{f}}{\frac{1}{f\cdot g}}\) otrzymując symbol nieoznaczony \(\frac{0}{0}\).
4. Gdy \(f^g\to\left[1^\infty\right]\) lub \([0^\infty]\) lub \([0^0]\), to możemy zastosować tożsamość \(f^g=e^{g\ln f}\) otrzymując symbol nieoznaczony \(0\cdot \infty\), który dalej można przekształcić do symbolu \(\frac{0}{0}\) lub \(\frac{\infty}{\infty}\) (patrz punk 1).

Komentarzy (0)