Oblicz granicę funkcji
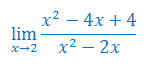
Rozwiązanie

Wskazówki
Korzystamy z faktu, że
\(x^2-4x+4=x^2-2\cdot 2x+2^2=(x-2)^2\)
oraz
\(x^2-2x=x(x-2)\).
Uwaga:
Zadanie można rozwiązać też stosując regułę de L'Hospitala.
Jak radzić sobie z granicami niewłaściwymi?
Granica z wyrażenia: liczba + "nieskończoność" = "nieskończoność"
\(g+\infty=\infty+g=\infty,\,\,gdy\,\,-\infty<g\le \infty\)
Granica z wyrażenia: liczba razy "nieskończoność" = "nieskończoność"
\(g\cdot\infty=\infty\cdot g=\infty,\,\,gdy\,\,0<g\le \infty\)
Granica z wyrażenia: liczba dzielona przez "nieskończoność" = 0
\(\frac{g}{\infty}=0,\,\,gdy\,\,-\infty<g<\infty\)
Granica z wyrażenia: liczba dzielona przez 0 = "nieskończoność"
\(\frac{g}{0^+}=\infty,\,\,gdy\,\,0<g<\infty\)
Granica z wyrażenia: liczba do potęgi "nieskończoność" = 0, gdy liczba jest dodatnia i mniejsza od 1
\(g^{\infty}=0,\,\,gdy\,\,0<g<1\)
Granica z wyrażenia: liczba do potęgi "nieskończoność" = "nieskończoność", gdy liczba jest większa od 1
\(g^{\infty}=\infty,\,\,gdy\,\,1<g\le \infty\)
Granica z wyrażenia: "nieskończoność" do potęgi liczba = 0, gdy liczba jest ujemna
\(\infty^{g}=0,\,\,gdy\,\,-\infty<g< 0\)
Granica z wyrażenia: "nieskończoność" do potęgi liczba = "nieskończoność", gdy liczba jest dodatnia
\(\infty^{g}=\infty,\,\,gdy\,\,0<g\le \infty\)

Komentarzy (0)