Korzystając z twierdzenia o trzech funkcjach oblicz granicę
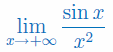
Rozwiązanie

Wskazówki
W rozwiązaniu korzystamy z nierówności:
\[-1\le \sin(x)\le 1\]
Twierdzenie o trzech funkcjach
Jeżeli funkcje f(x), g(x), h(x) spełniają warunki
- \(f(x)\le g(x)\le h(x)\) (w pewnym otoczeniu punktu \(x_0\))
- \(\lim\limits_{x\to x_0}f(x)=\lim\limits_{x\to x_0} h(x)=g\)
(\(x_0\) może być liczbą lub może być równe \(\infty\))
to \(\lim\limits_{x\to x_0}g(x)=g.\)
Jak radzić sobie z granicami niewłaściwymi?
Granica z wyrażenia: liczba + "nieskończoność" = "nieskończoność"
\(g+\infty=\infty+g=\infty,\,\,gdy\,\,-\infty<g\le \infty\)
Granica z wyrażenia: liczba razy "nieskończoność" = "nieskończoność"
\(g\cdot\infty=\infty\cdot g=\infty,\,\,gdy\,\,0<g\le \infty\)
Granica z wyrażenia: liczba dzielona przez "nieskończoność" = 0
\(\frac{g}{\infty}=0,\,\,gdy\,\,-\infty<g<\infty\)
Granica z wyrażenia: liczba dzielona przez 0 = "nieskończoność"
\(\frac{g}{0^+}=\infty,\,\,gdy\,\,0<g<\infty\)
Granica z wyrażenia: liczba do potęgi "nieskończoność" = 0, gdy liczba jest dodatnia i mniejsza od 1
\(g^{\infty}=0,\,\,gdy\,\,0<g<1\)
Granica z wyrażenia: liczba do potęgi "nieskończoność" = "nieskończoność", gdy liczba jest większa od 1
\(g^{\infty}=\infty,\,\,gdy\,\,1<g\le \infty\)
Granica z wyrażenia: "nieskończoność" do potęgi liczba = 0, gdy liczba jest ujemna
\(\infty^{g}=0,\,\,gdy\,\,-\infty<g< 0\)
Granica z wyrażenia: "nieskończoność" do potęgi liczba = "nieskończoność", gdy liczba jest dodatnia
\(\infty^{g}=\infty,\,\,gdy\,\,0<g\le \infty\)

Komentarzy (0)