Oblicz granicę funkcji korzystając z reguły de L'Hospitala
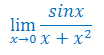
Rozwiązanie
Do obliczenia granicy stosujemy regułę de L'Hospitala, w tym celu liczymy pochodne funkcji stojących w liczniku i mianowniku:

Wskazówki
W rozwiązaniu korzystamy z reguły de L'Hospitala (piszemy wtedy duże H nad znakiem równości, tak jak w rozwiązaniu przykładu)
\(\lim\limits_{x\to 0} \frac{\sin x}{x+x^2}=\left[\frac{0}{0}\right]\stackrel{H}{=}\lim\limits_{x\to 0} \frac{(\sin x)'}{(x+x^2)'}=\lim\limits_{x\to 0} \frac{\cos x}{1+2x}=1\).
Po drugiej równości stosujemy regułę de L'Hospitala, liczymy pochodne z funkcji stojących w liczniku i mianowniku, na koniec liczymy granicę, która stanowi ostateczny wynik.
W rozwiązaniu korzystamy również z równości \(\sin 0=0\) i \(\cos 0 = 1\), podobnie \(\lim\limits_{x\to 0}\sin x=0\) i \(\lim\limits_{x\to 0}\cos x=1\).
Raguła de L'Hospitala - teoria
Jeżeli\[\lim\limits_{x\to x_0} \frac{f(x)}{g(x)}=\left[\frac{0}{0}\right]\,\,\,\textrm{lub}\,\,\,\left[\frac{\infty}{\infty}\right]\]istnieją pochodne f'(x) i g'(x) (w otoczeniu punktu \(x_0\)) oraz istnieje granica\[\lim\limits_{x\to x_0} \frac{f'(x)}{g'(x)}\]to\[\lim\limits_{x\to x_0} \frac{f(x)}{g(x)}=\lim\limits_{x\to x_0} \frac{f'(x)}{g'(x)}\]
UWAGA 1: Reguła de L'Hospitala "działa" też dla granic jednostronnych.
UWAGA 2: Reguła de L'Hospitala "NIE DZIAŁA" dla innych symboli nieoznaczonych, tj. \([\infty-\infty],\,\,\,[0\cdot \infty],\,\,\,\left[1^{\infty}\right],\,\,\,\left[\infty^{0}\right],\,\,\,\left[0^{0}\right]\)
Jak przekształcać "nieoznaczoności", aby uzyskać \(\frac{0}{0}\) lub \(\frac{\infty}{\infty}\)?
1. Gdy \(f\cdot g\to\left[0\cdot \infty\right]\), to możemy zastosować tożsamość \(f\cdot g=\frac{f}{\frac{1}{g}}\) otrzymując symbol nieoznaczony \(\frac{0}{0}\) lub \(\frac{\infty}{\infty}\).
2. Gdy \(\frac{1}{f}\pm \frac{1}{g}\to\left[\infty- \infty\right]\), to możemy zastosować tożsamość \(\frac{1}{f}\pm \frac{1}{g}=\frac{g\pm f}{f\cdot g}\) otrzymując symbol nieoznaczony \(\frac{0}{0}\).
3. Gdy \(f-g\to\left[\infty- \infty\right]\), to możemy zastosować tożsamość \(f-g=\frac{\frac{1}{g}-\frac{1}{f}}{\frac{1}{f\cdot g}}\) otrzymując symbol nieoznaczony \(\frac{0}{0}\).
4. Gdy \(f^g\to\left[1^\infty\right]\) lub \([0^\infty]\) lub \([0^0]\), to możemy zastosować tożsamość \(f^g=e^{g\ln f}\) otrzymując symbol nieoznaczony \(0\cdot \infty\), który dalej można przekształcić do symbolu \(\frac{0}{0}\) lub \(\frac{\infty}{\infty}\) (patrz punk 1).

Komentarzy (0)