Narysuj na płaszczyźnie zespolonej zbiór liczb zespolonych

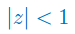
Rozwiązanie

Liczby zespolone spełniające naszą nierówność leżą w odległości mniejszej niż 1 od środka układu współrzędnych, czyli wewnątrz koła o środku w punkcie \(z_0=0\) i promieniu \(r=1\). Nierówność jest ostra, więc brzeg (czyli okrąg) nie należy do zbioru rozwiązań i należy zaznaczyć go linią przerywaną:

Wskazówki

Interpretacja geometryczna modułu liczby zespolonej

Moduł liczby zespolonej \(z=x+yi\) liczymy ze wzoru

\[|z|=\sqrt{x^2+y^2}\]

Moduł jest równy odległości liczby zespolonej \(z\) od początku (środka) układu współrzędnych. 

Nierówność \(|z-z_0|<r\) wyznacza zawsze zbiór liczb zespolonych \(z\) odległych od punktu \(z_0\) o odległość mniejszą niż \(r\).
Zbiór ten tworzy koło bez brzegu o środku w punkcie \(z_0\) i promieniu r.

Wyprowadzenie postaci zbioru rozwiązań nierówności \(|z-z_0|<r\)

Rozważmy ogólną nierówność \(|z-z_0|<r\), gdzie \(r>0\) (\(r\) jest liczbą rzeczywistą dodatnią), a \(z\) i \(z_0\) są liczbami zespolonymi, przy czym \(z_0\) jest znana i podana w treści zadania.

Niech \(z=x+yi\), \(z_0=x_0+y_0i\), wtedy

\[|z-z_0|=|x+yi-(x_0+y_0i)|=|(x-x_0)+(y-y_0)i|=\sqrt{(x-x_0)^2+(y-y_0)^2}\]

Zatem wychodząc od nierównośći \(|z-z_0|<r\) otrzymujemy równoważną nierówność

\[\sqrt{(x-x_0)^2+(y-y_0)^2}<r\]

Podnosząc obie strony do kwadratu uzyskujemy nierówność opisującą koło bez brzegu o środku w punkcie \(S=(x_0,y_0)=z_0\) i promieniu równym \(r\)

\[(x-x_0)^2+(y-y_0)^2<r^2\]

• « Poprzednie

Komentarzy (0)

• Imię
• E-mail (niewidoczny)
• Komentarz

WYŚLIJ