Dla jakich wartości parametru a funkcja jest ciągła w punkcie x=4
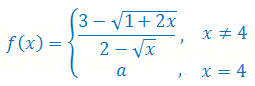
Rozwiązanie

Na koniec wykres funkcji \(f(x)\) (widać, że funkcja jest ciągła):
Wskazówki
Przy liczeniu granicy korzystamy ze wzoru skróconego mnożenia:
\[(a-b)(a+b)=a^2-b^2\]
stąd:
\[(2-\sqrt{x})(2+\sqrt{x})=2^2-(\sqrt{x})^2=4-x\]
\[(3-\sqrt{1+2x})(3+\sqrt{1+2x})=3^2-(\sqrt{1+2x})^2=9-(1+2x)=8-2x=2(4-x)\]
Warunek ciągłości funkcji
Funkcja jest ciągła w punkcie \(x_0\), gdy spełniony jest warunek
\(\lim\limits_{x\to x_0} f(x)=f(x_0)\).
Jakie funkcje są ciągłe?
Ciągłe (w swoich dziedzinach) są wszystkie funkcje elementarne (czyli takie, które da się zapisać wzorem):
- wielomiany, np. \(f(x)=5, f(x)=x, f(x)=3x^3-7x^2+2\)
- funkcje wymierne postaci \(\frac{f(x)}{g(x)}\), gdzie f(x) i g(x) są wielomianami
- funkcja wykładnicza \(f(x)=a^x, a>0\)
- funkcja potęgowa \(f(x)=x^a\), np. \(f(x)=\sqrt{x}\)
- funkcja logarytmiczna \(f(x)=\log_a(x),\, a>0,\, a\neq 1\)
- funkcje trygonometryczne: sinx, cosx, tgx i ctgx
- funkcje cyklometryczne: arcsinx, arccosx, arctgx i arcctgx
Własności funkcji ciągłych
Jeżeli funkcje f(x) i g(x) są ciągłe, to funkcje
- \(f(x)+g(x)\) - suma funkcji
- \(f(x)-g(x)\) - różnica funkcji
- \(f(x)g(x)\) - iloczyn funkcji
- \(\frac{f(x)}{g(x)}\) - iloraz funkcji
- \(f(g(x))\) - złożenie funkcji (superpozycja)
też są ciągłe.

Komentarzy (0)