Wyznacz wszystkie asymptoty funkcji
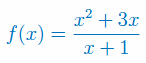
Rozwiązanie
W tego typu zadaniach zaczynamy zawsze od wyznaczenia dziedziny funkcji:


Na koniec wykres funkcji \(f(x)=\frac{x^2+3x}{x+1}\) (na czerwono).
Wszystkie asymptoty funkcji zaznaczone są kolorem niebieskim:
Wskazówki
Asymptoty pionowe
Są to proste zadane przez równanie postaci \(x=x_0\), gdzie \(x_0\) jest punktem nienależącym do dziedziny funkcji.
Istnienie asymptoty pionowej sprawdzamy licząc granice jednostronne w punktach leżących na "krańcach dziedziny":
\(\lim\limits_{x\to x_0^+} f(x)\) i \(\lim\limits_{x\to x_0^-} f(x)\),
gdzie \(x_0\) jest punktem nienależącym do dziedziny funkcji f(x).
Asymtoty poziome i ukośne
Są to proste zadane przez równanie postaci \(y=ax+b\).
Współczynniki a i b liczymy ze wzorów:
\(a=\lim\limits_{x\to \pm\infty} \frac{f(x)}{x}\),
\(b=\lim\limits_{x\to \pm\infty} \left(f(x)-ax\right)\).

Komentarzy (2)
\[\frac{x^2+3x}{x+1}-x=\frac{x^2+3x}{x+1}-\frac{x(x+1)}{x+1}=\frac{x^2+3x-x^2-x}{x+1}=\frac{2x}{x+1}\]
więc wygląda na to, że wszystko jest policzone dobrze :-)