Podaj wzór na granicę

Granice ciągów - zad. 27

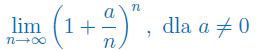
Rozwiązanie

Wzór wygląda następująco:

Granica ciągu liczbowego - zad. 27 - rozwiązanie

gdzie literka e oznacza liczbę Eulera (zwana jest też liczbą Neppera), która w przybliżeniu wynosi 2,72.

Stała e stanowi podstawę logarytmu naturalnego:

\(\log_e x=\ln x\).

Jest to wzór, którego warto nauczyć się na pamięć, ponieważ przydaje się bardzo często:-)

Gdy a=1, to otrzymujemy znaną granicę z liczbą e:

Granica ciągu z liczbą e Natomiast gdy a=-1, to otrzymujemy wzór na granicę:

Granica ciągu liczbowego z liczbą e

Dużym błędem byłoby uznanie, że \(\frac{a}{n}\to 0\) przy \(n\to\infty\) i napisanie tej granicy w następujący sposób:

\[\lim\limits_{n\to\infty} \left(1+\frac{a}{n}\right)^n=\lim\limits_{n\to\infty} 1^n=1\,-\,\textrm{źle!!!}\]