Oblicz pochodną funkcji
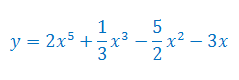
Rozwiązanie
Pochodna funkcji wynosi:

Wskazówki
W rozwiązaniu wykorzystujemy wzór:
\((x^n)'=nx^{n-1}\)
oraz fakt, że pochodna sumy (lub różnicy) funkcji jest równa sumie (lub różnicy) pochodnych:
\((f(x)+g(x))'=f'(x)+g'(x)\)
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
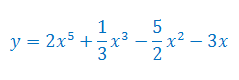
Pochodna funkcji wynosi:

W rozwiązaniu wykorzystujemy wzór:
\((x^n)'=nx^{n-1}\)
oraz fakt, że pochodna sumy (lub różnicy) funkcji jest równa sumie (lub różnicy) pochodnych:
\((f(x)+g(x))'=f'(x)+g'(x)\)
Komentarzy (0)