Oblicz pochodną funkcji
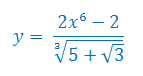
Rozwiązanie
Pochodna funkcji wynosi:

Wskazówki
W rozwiązaniu wykorzystujemy wzory:
\((af(x))'=af'(x),\,\,a=const\)
\((x^n)'=nx^{n-1}\)
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
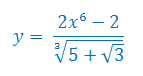
Pochodna funkcji wynosi:

W rozwiązaniu wykorzystujemy wzory:
\((af(x))'=af'(x),\,\,a=const\)
\((x^n)'=nx^{n-1}\)
Komentarzy (2)
Oto rozwiązanie z zastosowaniem wzoru na pochodną ilorazu funkcji:\[\left(\frac{2x^6-2}{\sqrt[3]{5+\sqrt{3}}}\right)'=\frac{(2x^6-2)'\cdot (\sqrt[3]{5+\sqrt{3}})-(2x^6-2)\cdot (\sqrt[3]{5+\sqrt{3}})'}{(\sqrt[3]{5+\sqrt{3}})^2}=\]\[=\frac{(12x^5-0)\cdot (\sqrt[3]{5+\sqrt{3}})-(2x^6-2)\cdot 0}{(\sqrt[3]{5+\sqrt{3}})^2}=\frac{12x^5\cdot (\sqrt[3]{5+\sqrt{3}})}{(\sqrt[3]{5+\sqrt{3}})^2}=\frac{12x^5}{\sqrt[3]{5+\sqrt{3}}}\]Może Pan porównać stopień skomplikowania obu rozwiązań, widać, że to pierwsze jest krótsze. Stąd wniosek, że zawsze warto uprościć wyrażenie zanim zaczniemy stosować jakieś wzory :-)