Zbadaj zbieżność szeregu liczbowego
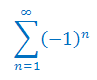
Rozwiązanie
Sprawdzimy, czy spełniony jest warunek konieczny zbieżności szeregów liczbowych:

Wskazówki do zadania
Granica ciągu \(a_n=(-1)^n\) nie istnieje, ponieważ można wybrać dwa podciągi zbieżne do różnych granic.
Weźmy podciąg \(a_{2k}=(-1)^{2k}=1\), dla \(k=1,2,3,...\), wówczas:
\[\lim\limits_{k\to \infty} a_{2k}=\lim\limits_{k\to \infty} 1=1\]
Weźmy podciąg \(a_{2k+1}=(-1)^{2k+1}=-1\), dla \(k=1,2,3,...\), wówczas:
\[\lim\limits_{k\to \infty} a_{2k+1}=\lim\limits_{k\to \infty} (-1)=-1\]
Granice podciągów są różne, więc granica ciągu \(a_n=(-1)^n\) nie istnieje.
Warunek konieczny zbieżności szeregów liczbowych
Jeżeli \(\lim\limits_{n\to\infty} a_n\neq 0\) lub \(\lim\limits_{n\to\infty} a_n\) nie istnieje, to szereg \(\sum\limits_{n=1}^\infty a_n\) jest rozbieżny.
Jak sprawdzić, czy szereg liczbowy jest zbieżny?
Oto podstawowe metody, które można wykorzystać do sprawdzania zbieżności szeregów liczbowych:
1. Sprawdzenie, czy spełniony jest warunek konieczny zbieżności. Jeżeli:
\[\lim\limits_{n\to\infty} a_n\neq 0\]
to szereg jest rozbieżny (warunek konieczny pozwala stwierdzić jedynie czy szereg jest rozbieżny).
2. Obliczenie granicy ciągu sum częściowych szeregu \(S_n=\sum\limits_{k=0}^n a_k\).
Szereg jest zbieżny, gdy jego ciąg sum częściowych jest zbieżny:
\[\sum\limits_{k=0}^\infty a_k=\lim\limits_{n\to \infty} \sum\limits_{k=0}^n a_k=\lim\limits_{n\to \infty}S_n\]
3. Wykorzystanie jednego z kryteriów zbieżności szeregów:
(a) kryterium porównawcze
(b) kryterium ilorazowe
(c) kryterium Cauchy'ego
(d) kryterium d'Alemberta
(e) kryterium całkowe
(f) inne kryteria (m.in. Abela i Dirichleta)

Komentarzy (0)