Oblicz granicę ciągu
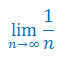
Rozwiązanie
Jest to bardzo prosta granica, która wynosi:

Poniżej możesz zobaczyć zachowanie ciągu \(a_n=\frac{1}{n}\) na wykresie:

Wskazówki
Patrzymy do czego zbiega licznik i mianownik:
- licznik zbiega do jedynki (w liczniku mamy ciąg stały \(a_n=1\));
- mianownik zbiega do nieskończoności (w mianowniku mamy ciąg \(b_n=n\), który rośnie wraz z indeksem n aż do nieskończoności),
Do wyznaczenia granicy możemy wykorzystać następujący schemat:
\[\frac{g}{\infty}=0,\,\,gdy\,\,-\infty<g<\infty\]
(liczba dzielona przez "nieskończoność" = 0)
Zatem nasza granica wynosi 0.
Jak radzić sobie z nieskończonościami w granicach?
Gdy w granicy występuje \(\infty\) lub \(-\infty\), to stosuje się następujące schematy:
Granica ciągu: liczba + "nieskończoność" = "nieskończoność"
\(g+\infty=\infty+g=\infty,\,\,gdy\,\,-\infty<g\le \infty\)
Granica ciągu: liczba razy "nieskończoność" = "nieskończoność"
\(g\cdot\infty=\infty\cdot g=\infty,\,\,gdy\,\,0<g\le \infty\)
Granica ciągu: liczba dzielona przez "nieskończoność" = 0
\(\frac{g}{\infty}=0,\,\,gdy\,\,-\infty<g<\infty\)
Granica ciągu: liczba dzielona przez 0 = "nieskończoność"
\(\frac{g}{0}=\infty,\,\,gdy\,\,0<g<\infty\)
Granica ciągu: liczba do potęgi "nieskończoność" = 0, gdy liczba jest dodatnia i mniejsza od 1
\(g^{\infty}=0,\,\,gdy\,\,0<g<1\)
Granica ciągu: liczba do potęgi "nieskończoność" = "nieskończoność", gdy liczba jest większa od 1
\(g^{\infty}=\infty,\,\,gdy\,\,1<g\le \infty\)
Granica ciągu: "nieskończoność" do potęgi liczba = 0, gdy liczba jest ujemna
\(\infty^{g}=0,\,\,gdy\,\,-\infty<g< 0\)
Granica ciągu: "nieskończoność" do potęgi liczba = "nieskończoność", gdy liczba jest dodatnia
\(\infty^{g}=\infty,\,\,gdy\,\,0<g\le \infty\)
Jak liczyć granice ciągów - użyteczne własności
Jeżeli ciągi \(a_n\) i \(b_n\) są zbieżne do granic właściwych (skończonych liczb), to
\(\lim\limits_{n\to \infty}(a_n+b_n)=\lim\limits_{n\to \infty} a_n+\lim\limits_{n\to \infty} b_n\)
\(\lim\limits_{n\to \infty}(a_n-b_n)=\lim\limits_{n\to \infty} a_n-\lim\limits_{n\to \infty} b_n\)
\(\lim\limits_{n\to \infty}(c\cdot a_n)=c\cdot \lim\limits_{n\to \infty} a_n\), gdy \(c\in\mathbb{R}\)
\(\lim\limits_{n\to \infty}(a_n\cdot b_n)=\left(\lim\limits_{n\to \infty} a_n\right)\cdot \left(\lim\limits_{n\to \infty}b_n\right)\)
\(\lim\limits_{n\to \infty}\left(\frac{a_n}{b_n}\right)=\frac{\lim\limits_{n\to \infty} a_n}{\lim\limits_{n\to \infty} b_n}\), gdy \(\lim\limits_{n\to \infty} b_n\neq 0\)
\(\lim\limits_{n\to \infty}(a_n)^p=\left(\lim\limits_{n\to \infty} a_n\right)^p\),
gdy p jest liczbą całkowitą różną od zera
\(\lim\limits_{n\to \infty}\sqrt[k]{a_n}=\sqrt[k]{\lim\limits_{n\to \infty} a_n}\),
gdy k jest liczbą naturalną różną od 1

Komentarzy (0)