Start Używając metody bezwyznacznikowej wyznacz macierz odwrotną do macierzy:
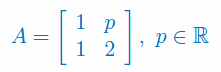
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Kategorie zadań z rozwiązaniami z matematyki wyższej
- Pochodne funkcji (122)
- Całki (215)
- Całki nieoznaczone (121)
- Całki oznaczone (32)
- Całki niewłaściwe (24)
- Całki podwójne (16)
- Całki potrójne (8)
- Całki krzywoliniowe (14)
- Funkcje (145)
- Szeregi i ciągi liczbowe (115)
- Ciągi liczbowe (20)
- Granice ciągów (38)
- Szeregi liczbowe (36)
- Szeregi potęgowe i funkcyjne (17)
- Szeregi Fouriera (4)
- Równania różniczkowe (44)
- Macierze i wyznaczniki (90)
- Działania na macierzach (22)
- Wyznacznik macierzy (24)
- Macierz odwrotna (16)
- Równania macierzowe (14)
- Rząd macierzy (10)
- Wartości i wektory własne (4)
- Liczby zespolone (134)
- Wielomiany (37)
- Równania i nierówności (3)
- Układy równań liniowych (29)
- Geometria analityczna (34)
- Logika (44)
- Zdania logiczne (22)
- Działania na zbiorach (22)
- Rachunek prawdopodobieństwa (84)
- Kombinatoryka (36)
- Prawdopodobieństwo (38)
- Zmienna losowa (6)
- Funkcja charakterystyczna (4)
- Statystyka matematyczna (5)
- Finanse (6)
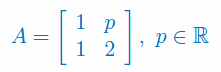
Oblicz macierz odwrotną do macierzy stopnia 4:
\(\begin{bmatrix}1&2&3&4\\2&3&1&2\\1&1&1&-1\\1&0&-2&-6\end{bmatrix}\)
Sprawdź czy macierz:
\(\begin{bmatrix}22&-6&-26&17\\-17&5&20&-13\\-1&0&2&-1\\4&-1&-5&3\end{bmatrix}\)
jest macierzą odwrotną do macierzy:
\(\begin{bmatrix}1&2&3&4\\2&3&1&2\\1&1&1&-1\\1&0&-2&-6\end{bmatrix}\)
Korzystając z definicji równości macierzy wyznacz liczby a,b,c,d
\(\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}\)
Korzystając z definicji równości macierzy rozwiąż równanie macierzowe (znajdź a i b)
\({\begin{bmatrix} a & -2 & 1+a \\ b+1 & 0 & 1\\ a+b & 1 &b \end{bmatrix}=\begin{bmatrix} a & a-b& b-1\\ b+1 & a+b& b\\0&1&-a \end{bmatrix}}\)
Rozwiąż równanie macierzowe:
\(2A+3X=B\)
gdzie A i B są dowolnymi macierzami stopnia n.
Znajdź macierz X spełniającą równanie macierzowe:
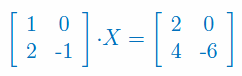
Znajdź wszystkie macierze X spełniające równanie macierzowe:
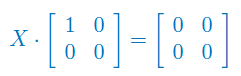
Znajdź macierz X spełniającą równanie macierzowe:
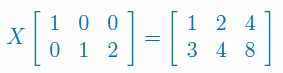
Znajdź macierz X spełniającą równanie macierzowe:
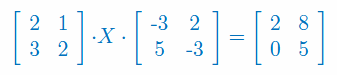
Rozwiąż równanie macierzowe:
\(A\cdot B=I\)
gdzie A jest macierzą wymiaru 1x2, a B macierzą o wymiarach 2x1 (I jest macierzą jednostkową).
Rozwiąż równanie macierzowe:
\(\begin{bmatrix} -1 & 2 \\1 & 0\end{bmatrix}\cdot (X+I)=\begin{bmatrix} -1 & 2\\ 1&0\end{bmatrix}\cdot X-X\)
Wyznacz elementy macierzy X, jeżeli:
\(2X\begin{bmatrix} -1 & 1 \\1 & -2\end{bmatrix}^T+5I=\begin{bmatrix} 3 & 1\\ 1&2\end{bmatrix}\begin{bmatrix}3&-5\\-2&4\end{bmatrix}^T\)
Rozwiąż równanie macierzowe:
\(A\cdot X\cdot A^{-1}=I\)
gdzie A jest dowolną macierzą nieosobliwą stopnia n, a I to macierz jednostkowa stopnia n.
Rozwiąż równanie macierzowe:
\(A^{-1}\cdot X\cdot C^{-1}=B\)
gdzie B, C to macierze nieosobliwe stopnia 3, takie, że \(B\cdot C=A^2\) oraz:
\(A=\begin{bmatrix}1&0&0\\0&2&0\\0&0&3\end{bmatrix}\)
Rozwiąż równanie macierzowe:
\(\begin{bmatrix}1&-3\\2&-2\\3&-1\end{bmatrix}^T\begin{bmatrix}0&-1\\-1&1\\1&0\end{bmatrix}-2\left(\begin{bmatrix}-2&4\\-1&2\end{bmatrix}^2+X\right)=(X^T+I^2)^T\)
Wyznacz elementy macierzy X, jeżeli:
\(X\cdot \begin{bmatrix}1&2&3&4\\2&3&1&2\\1&1&1&-1\\1&0&-2&-6\end{bmatrix}=\begin{bmatrix}1&0&0&1\\0&0&1&0\\0&1&0&0\\1&0&0&0\end{bmatrix}\)
Podaj wszystkie minory macierzy:
\(A=\begin{bmatrix}1&2\\1&0\end{bmatrix}\)
Następnie określ rząd macierzy A.
Podaj przykład macierzy kwadratowej, której rząd jest równy 1.
Oblicz rząd macierzy:
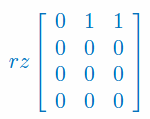
Oblicz rząd macierzy:
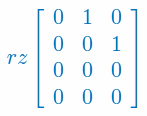
Podaj wszystkie minory macierzy:
\(A=\begin{bmatrix}0&3&-1\\2&0&1\end{bmatrix}\)
Następnie określ rząd macierzy A.
Oblicz rząd macierzy:
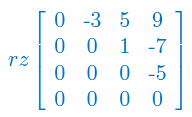
Oblicz rząd macierzy:
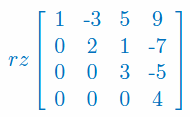
Oblicz rząd macierzy:
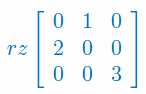
Oblicz rząd macierzy:
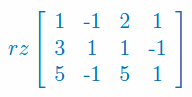
Oblicz rząd macierzy w zależności od parametru p:
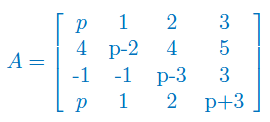
Wyznacz wartości i wektory własne macierzy:
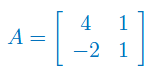
Wyznacz wartości i wektory własne macierzy stopnia 4
\(A=\left[\begin{array}{cccc}1&0&0&0\\0&2&0&0\\0&0&3&0\\0&0&0&4\end{array}\right]\)
Wyznacz wartości i wektory własne macierzy:
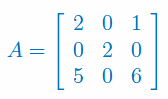
Wyznaczyć wartości własne \(\lambda_1\neq \lambda_2\) macierzy A wiedząc, że
\(\det A=2,\,\,\,\,tr A=3\)
Podaj część rzeczywistą i urojoną liczby zespolonej z:
\(z=2-i\)
Podaj część rzeczywistą i urojoną liczby zespolonej z:
\(z=2i\)
Podaj część rzeczywistą i urojoną liczby zespolonej z:
\(z=-6\)
Oblicz:
\(i+2i\)
Wykonaj działania na liczbach zespolonych:
\(\frac{1}{2}+i-\left(2+\frac{1}{2}i\right)\)
Wykonaj mnożenie liczb zespolonych:
\((3-\sqrt{2}i)(-1-i)\)
Wykonaj dzielenie liczb zespolonych:
\(\frac{1}{i}\)
Wykonaj dzielenie liczb zespolonych:
\(\frac{1}{1+i}\)
Wykonaj dzielenie:
\(\frac{1}{z}\)
wiedząc, że \(z=x+yi\), gdzie \(x,y\in\mathbb{R}\).
Wykonaj potęgowanie jednostki urojonej:
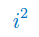
Wykonaj potęgowanie jednostki urojonej:
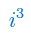
Wykonaj potęgowanie jednostki urojonej:
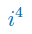
Wykonaj działanie na liczbach zespolonych:
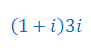
Wykonaj działania na liczbach zespolonych:
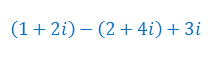
Wykonaj mnożenia liczb zespolonych:
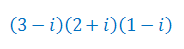
Oblicz potęgę liczby zespolonej:
\((1+i)^8\)
Oblicz potęgę liczby zespolonej:
\((2-i)^2\)
Wykonaj potęgowanie:
\((1-i)^3\)
Wykonaj potęgowanie jednostki urojonej:
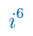
Na tej stronie znajdziesz około tysiąca zadań z rozwiązaniami i przykładów krok po kroku głównie z zakresu matematyki wyższej, jak również z matematyki na poziomie liceum. Zadania podzielone są na działy tematyczne zazwyczaj według przedmiotów i tematów wymaganych na studiach, np. zadania z pochodnych funkcji i całek (analiza matematyczna), macierzy i liczb zespolonych (algebra liniowa), zmiennych losowych i prawdopodobieństwa (rachunek prawdopodobieństwa) itd.
W każdej kategorii znajdziesz zadania o różnym poziomie trudności, a pod każdym zadaniem znajdziesz wiele wskazówek jak przebiega rozwiązanie, potrzebne definicje i wzory oraz podsumowanie schematów użytych w rozwiązaniu. Często rozwiązanie zadania omówione jest wręcz krok po kroku. Warto starać się samodzielnie rozwiązać jak najwięcej zadań znajdujących się na stronie, ponieważ są tu zebrane typowe zadania z kolokwiów i egzaminów z polskich uczelni. Nauka matematyki na przykładach i konkretnych zadaniach jest najbardziej efektywna - potwierdzają to badania naukowe. Trzeba tylko uczyć się (a właściwie analizować przykłady i rozwiązywać zadania) konsekwentnie i wytrwale, a efekty w postaci lepszego zrozumienia pojęć i schematów oraz umiejętność samodzielnego rozweiązywania podobnych zadań przyjdą same.
Pamiętaj, że zawsze masz możliwość zadania pytania w komentarzu pod każdym zadaniem - warto z tej możliwości korzystać, ponieważ na tej stronie nie ma głupich pytań i każde, nawet najgłupsze pytanie znajdzie swoją odpowiedź. Powodzenia w zrozumieniu matematyki!