Start Wyznacz dziedzinę i narysuj wykres funkcji
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Kategorie zadań z rozwiązaniami z matematyki wyższej
Funkcje - zadania z rozwiązaniami
Oblicz miejsca zerowe funkcji
\(f(x)=\frac{(x-1)(x+2)}{\sqrt{x}-1}\)
Wyznacz dziedzinę, miejsca zerowe i zbiór wartości funkcji wymiernej
\(f(x)=\frac{2}{x+3}+4\)
Określ dziedzinę funkcji
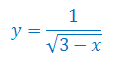
Określ dziedzinę funkcji (dla \(x\in\mathbb{R}\))
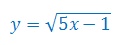
Określ dziedzinę funkcji
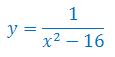
Podaj przykład funkcji wymiernej, która dla argumentu równego 1 przyjmuje wartość 5, a jej dziedziną jest zbiór:
\(D_f=\mathbb{R}\setminus \{0\}\)
Podaj przykład funkcji, której dziedziną jest zbiór liczb rzeczywistych dodatnich.
Wyznacz dziedzinę funkcji
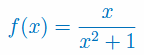
Wyznacz dziedzinę funkcji
\(f(x)=\ln(|x|)\)
Wyznacz dziedzinę i narysuj wykres funkcji
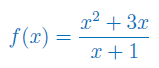
Wyznacz dziedzinę i narysuj wykres funkcji
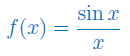
Wyznacz dziedzinę funkcji
Wyznacz dziedzinę funkcji
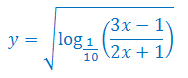
Oblicz miejsca zerowe wielomianu
\(f(x)=x^3-3x^2+2\)
Wyznacz dziedzinę funkcji
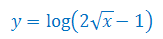
Wyznacz dziedzinę funkcji
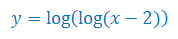
Wyznacz dziedzinę funkcji
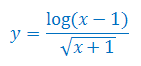
Wyznacz dziedzinę funkcji
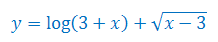
Wyznacz dziedzinę funkcji
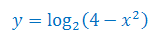
Wyznacz dziedzinę funkcji
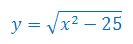
Podaj przykład funkcji, której dziedziną jest przedział:
\([0,1]\)
Wyznacz dziedzinę funkcji
\((a)\,\, f(x)=\ln(|x|+1)\)
\((b)\,\, f(x)=\ln(|x|-1)\)
Wyznacz dziedzinę funkcji
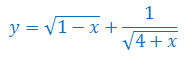
Wyznacz dziedzinę funkcji
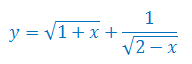
Wyznacz dziedzinę funkcji
\(f(x)=\ln(|x|)+\frac{1}{x-1}\)
Korzystając z twierdzeń o arytmetyce granic funkcji oblicz
\(\lim\limits_{x\to \pi}x^2\sin(x)\)
Korzystając z twierdzeń o arytmetyce granic niewłaściwych oblicz
\(\lim\limits_{x\to -\infty}5x^2\)
Korzystając z twierdzeń o arytmetyce granic funkcji oblicz
\(\lim\limits_{x\to 0}e^{\sin(x)}\)
Korzystając z twierdzeń o arytmetyce granic niewłaściwych oblicz
\(\lim\limits_{x\to \infty}\left(x+\frac{1}{x^2}\right)\)
Korzystając z twierdzeń o arytmetyce granic funkcji oblicz
\(\lim\limits_{x\to 0}\frac{x^2+1}{3\cos(x)}\)
Korzystając z twierdzeń o arytmetyce granic niewłaściwych oblicz
\(\lim\limits_{x\to 0}\frac{16}{x^2}\)
Korzystając z twierdzeń o arytmetyce granic niewłaściwych oblicz
\(\lim\limits_{x\to 0}\left(\sin x+\frac{1}{x^2}\right)\)
Korzystając z twierdzeń o arytmetyce granic niewłaściwych oblicz
\(\lim\limits_{x\to \infty}\left(\frac{1}{2}\right)^{\ln x}\)
Korzystając z własności granic funkcji oblicz
\(\lim\limits_{x\to 0}(2x+\sin(x^2))\)
Korzystając z reguły de L'Hospitala udowodnij, że
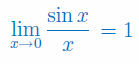
Oblicz granicę niewłaściwą funkcji
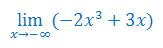
Korzystając z reguły de L'Hospitala oblicz granicę jednostronną funkcji
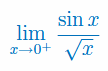
Korzystając z reguły de L'Hospitala udowodnij, że
\(\lim\limits_{x\to 0} \frac{\ln(x+1)}{x}=1\)
Oblicz granicę funkcji
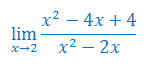
Korzystając z twierdzenia o trzech funkcjach oblicz granicę
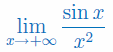
Korzystając z twierdzenia o dwóch funkcjach uzasadnić, że
\(\lim\limits_{x\to \infty}(\sin x-e^x)=-\infty\)
Oblicz granicę funkcji korzystając z reguły de L'Hospitala
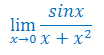
Oblicz granicę funkcji
\(\lim\limits_{x\to \infty} \frac{\ln x}{x}\)
Sprawdź, czy przy \(x\to 1\) istnieje granica funkcji
\(f(x)=\left\{\begin{array}{ccc}x&,\,\,\textrm{gdy}&x<1\\x+1&,\,\,\textrm{gdy}&x\ge 1\end{array}\right.\)
Korzystając z definicji Cauchy'ego granicy funkcji wykazać, że
\(\lim\limits_{x\to 0} \frac{1}{x^2}=+\infty\)
Korzystając z reguły de L'Hospitala uzasadnij, że dla każdej funkcji różniczkowalnej f(x)
\(\lim\limits_{x\to 0} \frac{\sin\big(f(x)\big)}{f(x)}=1,\,\,\,\textrm{gdy}\,\,\,\lim\limits_{x\to 0}f(x)=0\)
Korzystając z definicji Heinego granicy uzasadnij, że
\(\lim\limits_{x\to 0} x=0\)
Oblicz granicę funkcji \(f(x)\) w \(-\infty\) i \(+\infty\):
\(f(x)=\left\{\begin{array}{ll}\frac{1}{x}&\,\textrm{dla}\,\,x<1\\ 2-\frac{1}{x}&\,\textrm{dla}\,\,x\ge 1\end{array}\right.\)
Korzystając z reguły de L'Hospitala oblicz granicę funkcji:
\(\lim\limits_{x\to 0} \arcsin(3x)\cdot ctg(2x)\)
Jesteś w kategorii Funkcje zadania z rozwiązaniami
W tym dziele znajdziesz kilkadziesiąt zadań z rozwiązaniami krok po kroku z zakresu funkcji jednej zmiennej. Zobacz przykłady określania dziedziny i własności funkcji, obliczania granic, sprawdzania ciągłości funkcji, wyznaczania asymptot oraz sprawdzania monotoniczności i ekstremów. Ucząc się funkcji na przykładach poznasz typowe schematy rozwiązywania zadań, np. jak poradzić sobie z symbolami nieoznaczonymi przy obliczaniu granic funkcji (reguła de L'Hospitala), jak liczyć asymptoty funkcji i wiele innych. Pod większością zadań znajdziesz wyjaśnienie najważniejszych metod, schematów, pojęć i wzorów.
Zachęcam do próby samodzielnego rozwiązywania zadań z funkcji i sięganie do rozwiązań na stronie w ramach podpowiedzi lub w celu sprawdzenia wyniku. Jeśli czegoś nie rozumiesz zapytaj w komentarzu pod zadaniem - kto pyta nie błądzi i lepiej wyjaśnić wszystkie wątpliwości tak aby samemu potrafić rozwiązać podobne zadania. Na koiniec pozostaje mi jedynie życzyć Ci powodzenia w nauce i świetnych wyników na egzaminie!