Korzystając z twierdzeń o arytmetyce granic niewłaściwych oblicz
\(\lim\limits_{x\to -\infty}5x^2\)
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Korzystając z twierdzeń o arytmetyce granic niewłaściwych oblicz
\(\lim\limits_{x\to -\infty}5x^2\)
Korzystając z twierdzeń o arytmetyce granic niewłaściwych oblicz
\(\lim\limits_{x\to \infty}\left(\frac{1}{2}\right)^{\ln x}\)
Korzystając z twierdzeń o arytmetyce granic niewłaściwych oblicz
\(\lim\limits_{x\to 0}\frac{16}{x^2}\)
Korzystając z własności granic funkcji oblicz
\(\lim\limits_{x\to 0}(2x+\sin(x^2))\)
Korzystając z twierdzeń o arytmetyce granic funkcji oblicz
\(\lim\limits_{x\to \pi}x^2\sin(x)\)
Korzystając z twierdzeń o arytmetyce granic funkcji oblicz
\(\lim\limits_{x\to 0}\frac{x^2+1}{3\cos(x)}\)
Korzystając z twierdzeń o arytmetyce granic funkcji oblicz
\(\lim\limits_{x\to 0}e^{\sin(x)}\)
Korzystając z twierdzeń o arytmetyce granic niewłaściwych oblicz
\(\lim\limits_{x\to 0}\left(\sin x+\frac{1}{x^2}\right)\)
Korzystając z twierdzeń o arytmetyce granic niewłaściwych oblicz
\(\lim\limits_{x\to \infty}\left(x+\frac{1}{x^2}\right)\)
Korzystając z reguły de L'Hospitala udowodnij, że
\(\lim\limits_{x\to 0} \frac{\ln(x+1)}{x}=1\)
Korzystając z reguły de L'Hospitala oblicz granicę jednostronną funkcji
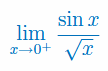
Korzystając z reguły de L'Hospitala udowodnij, że
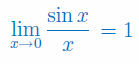
Oblicz granicę niewłaściwą funkcji
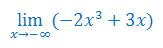
Oblicz granicę funkcji
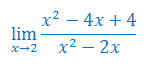
Korzystając z twierdzenia o dwóch funkcjach uzasadnić, że
\(\lim\limits_{x\to \infty}(\sin x-e^x)=-\infty\)
Korzystając z twierdzenia o trzech funkcjach oblicz granicę
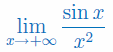
Oblicz granicę funkcji
\(\lim\limits_{x\to \infty} \frac{\ln x}{x}\)
Oblicz granicę funkcji korzystając z reguły de L'Hospitala
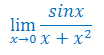
Sprawdź, czy przy \(x\to 1\) istnieje granica funkcji
\(f(x)=\left\{\begin{array}{ccc}x&,\,\,\textrm{gdy}&x<1\\x+1&,\,\,\textrm{gdy}&x\ge 1\end{array}\right.\)
Korzystając z definicji Cauchy'ego granicy funkcji wykazać, że
\(\lim\limits_{x\to 0} \frac{1}{x^2}=+\infty\)
Korzystając z definicji Heinego granicy uzasadnij, że
\(\lim\limits_{x\to 0} x=0\)
Korzystając z reguły de L'Hospitala uzasadnij, że dla każdej funkcji różniczkowalnej f(x)
\(\lim\limits_{x\to 0} \frac{\sin\big(f(x)\big)}{f(x)}=1,\,\,\,\textrm{gdy}\,\,\,\lim\limits_{x\to 0}f(x)=0\)
Oblicz granicę funkcji \(f(x)\) w \(-\infty\) i \(+\infty\):
\(f(x)=\left\{\begin{array}{ll}\frac{1}{x}&\,\textrm{dla}\,\,x<1\\ 2-\frac{1}{x}&\,\textrm{dla}\,\,x\ge 1\end{array}\right.\)
Wykaż, że
\(\lim\limits_{x\to 0} \frac{tg x}{x}=1\)
Korzystając z reguły de L'Hospitala oblicz granicę funkcji:
\(\lim\limits_{x\to 0} \arcsin(3x)\cdot ctg(2x)\)
Niech \(n\in\mathbb{R}\). Oblicz granicę funkcji:
\(\lim\limits_{x\to 0} \frac{\sin(n\cdot x)}{\sin(x)}\)
Oblicz granicę funkcji

Oblicz granicę funkcji:
\(\lim\limits_{x\to 0} \frac{\sin(2x)}{\sin(x)}\)
Korzystając z twierdzenia o trzech funkcjach wykaż, że:
\(\lim\limits_{x\to 0}x\sin \left(\frac{1}{x}\right)=0\)
Oblicz granicę funkcji
\(\lim\limits_{x\to \infty} \frac{\ln (x^2)}{\ln(x)}\)
Korzystając z twierdzenia o dwóch funkcjach uzasadnić, że
\(\lim\limits_{x\to 0^+}\frac{\ln x}{x}=-\infty\)
Oblicz granicę funkcji
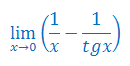
Oblicz granicę funkcji
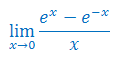
Oblicz granicę funkcji
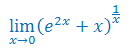
Oblicz granicę funkcji
\(\lim\limits_{x\to +\infty} \frac{\sqrt{x+1}-\sqrt{x}}{x}\)
Oblicz granicę funkcji
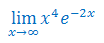
Oblicz granicę funkcji
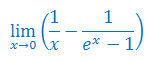
Oblicz granicę funkcji stosując regułę de L'Hospitala
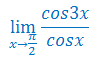
Oblicz granicę funkcji
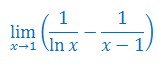
Oblicz granicę funkcji
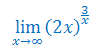
Oblicz granicę funkcji
\(\lim\limits_{x\to 1} \left(\frac{x}{x-1}-\frac{1}{\ln x}\right)\)
Oblicz granicę funkcji
\(\lim\limits_{x\to 0^+} x^x\)
Obliczyć granicę funkcji
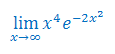
Oblicz granicę funkcji
\(\lim\limits_{x\to +\infty} \left(x-\ln x\right)\)
Oblicz granicę funkcji
\(\lim\limits_{x\to \infty} \frac{\ln (x)}{\sqrt{x}}\)
Obliczyć granicę niewłaściwą
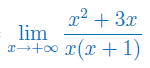
Obliczyć granicę funkcji
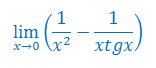
Korzystając z granic podstawowych wyrażeń nieoznaczonych oblicz granicę
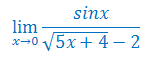
Korzystając z granic podstawowych wyrażeń nieoznaczonych oblicz granicę funkcji
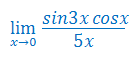
Oblicz granicę funkcji
Jesteś w kategorii Granice funkcji zadania z rozwiązaniami
W tym dziale znajdziesz przykłady i zadania dotyczące granic funkcji jednej zmiennej. Zobacz przykłady jak obliczać granice właściwe i niewłaściwe (w nieskończoności) funkcji elementarnych takich jak funkcje liniowe, wykładnicze, potęgowe, trygonometryczne czy logarytmiczne oraz funkcji złożonych.
Dzięki zgromadzonym na tej stronie przykładom poznasz metody obliczania granic obustronnych, jednostronnych właściwych i niewłaściwych, np. regułę de L'Hospitala, która pomaga obliczyć granice, w których występuje symbol nieoznaczony, twierdzenie o dwóch i trzech funkcjach oraz inne pomocne reguły.
Nauczysz się też obliczać granice z definicji (Heinego i Cauchyego) oraz przy użyciu gotowych wzorów, a także zobaczysz jak wykazać, że granica funkcji nie istnieje.
Pamiętaj, że jeśli masz problem ze zrozumieniem rozwiązania, to zawsze możesz zadać pytanie w komentarzu pod rozwiązaniem.