Korzystając z reguły de L'Hospitala udowodnij, że
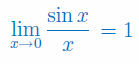
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Korzystając z reguły de L'Hospitala udowodnij, że
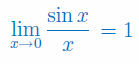
Korzystając z reguły de L'Hospitala oblicz granicę jednostronną funkcji
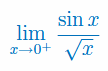
Korzystając z reguły de L'Hospitala udowodnij, że
\(\lim\limits_{x\to 0} \frac{\ln(x+1)}{x}=1\)
Oblicz granicę funkcji korzystając z reguły de L'Hospitala
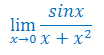
Korzystając z reguły de L'Hospitala uzasadnij, że dla każdej funkcji różniczkowalnej f(x)
\(\lim\limits_{x\to 0} \frac{\sin\big(f(x)\big)}{f(x)}=1,\,\,\,\textrm{gdy}\,\,\,\lim\limits_{x\to 0}f(x)=0\)
Niech \(n\in\mathbb{R}\). Oblicz granicę funkcji:
\(\lim\limits_{x\to 0} \frac{\sin(n\cdot x)}{\sin(x)}\)
Oblicz granicę funkcji:
\(\lim\limits_{x\to 0} \frac{\sin(2x)}{\sin(x)}\)
Wykaż, że
\(\lim\limits_{x\to 0} \frac{tg x}{x}=1\)
Korzystając z reguły de L'Hospitala oblicz granicę funkcji:
\(\lim\limits_{x\to 0} \arcsin(3x)\cdot ctg(2x)\)
Oblicz granicę funkcji
\(\lim\limits_{x\to 0^+} x^x\)
Oblicz granicę funkcji
\(\lim\limits_{x\to 1} \frac{x^2-1}{x-1}\)
Oblicz granicę funkcji
\(\lim\limits_{x\to 1} \left(\frac{x}{x-1}-\frac{1}{\ln x}\right)\)
Oblicz granicę funkcji
\(\lim\limits_{x\to +\infty} \left(x-\ln x\right)\)
Oblicz granicę funkcji
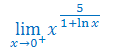
Oblicz granicę funkcji
\(\lim\limits_{x\to \infty} \frac{\ln (2x)}{\ln(x)}\)
Oblicz granicę funkcji
\(\lim\limits_{x\to \infty} \frac{\ln (x^2)}{\ln(x)}\)
Oblicz granicę funkcji
\(\lim\limits_{x\to \infty} \frac{\ln (x)}{\sqrt{x}}\)
Oblicz granicę funkcji
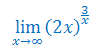
Oblicz granicę funkcji
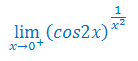
Obliczyć granicę funkcji
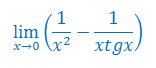
Obliczyć granicę funkcji
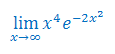
Obliczyć granicę funkcji
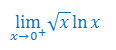
Obliczyć granicę funkcji
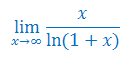
Oblicz granicę funkcji
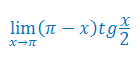
Oblicz granicę funkcji
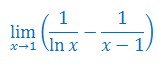
Oblicz granicę funkcji
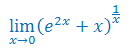
Oblicz granicę funkcji
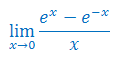
Oblicz granicę funkcji
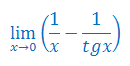
Oblicz granicę funkcji
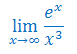
Oblicz granicę funkcji
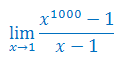
Oblicz granicę funkcji
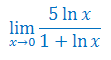
Oblicz granicę funkcji
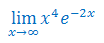
Oblicz granicę funkcji stosując regułę de L'Hospitala
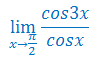
Jesteś w kategorii Granice funkcji zadania z rozwiązaniami
W tym dziale znajdziesz przykłady i zadania dotyczące granic funkcji jednej zmiennej. Zobacz przykłady jak obliczać granice właściwe i niewłaściwe (w nieskończoności) funkcji elementarnych takich jak funkcje liniowe, wykładnicze, potęgowe, trygonometryczne czy logarytmiczne oraz funkcji złożonych.
Dzięki zgromadzonym na tej stronie przykładom poznasz metody obliczania granic obustronnych, jednostronnych właściwych i niewłaściwych, np. regułę de L'Hospitala, która pomaga obliczyć granice, w których występuje symbol nieoznaczony, twierdzenie o dwóch i trzech funkcjach oraz inne pomocne reguły.
Nauczysz się też obliczać granice z definicji (Heinego i Cauchyego) oraz przy użyciu gotowych wzorów, a także zobaczysz jak wykazać, że granica funkcji nie istnieje.
Pamiętaj, że jeśli masz problem ze zrozumieniem rozwiązania, to zawsze możesz zadać pytanie w komentarzu pod rozwiązaniem.