Korzystając z definicji oblicz pochodną funkcji:
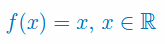
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Korzystając z definicji oblicz pochodną funkcji:
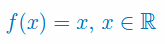
Korzystając z definicji oblicz pochodną funkcji:

Korzystając z definicji oblicz pochodną funkcji:

Korzystając z definicji (\(x\to x_0\)) oblicz pochodną funkcji:
\(f(x)=x^n,\,n\in\mathbb{N}\)
Korzystając z definicji zbadaj czy istnieje pochodna funkcji w punkcie \(x_0=0\):
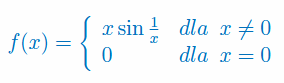
Korzystając z definicji wyprowadź wzór na pochodną iloczynu funkcji:
\((f(x)\cdot g(x))'=f'(x)g(x)+f(x)g(x)\)
Korzystając z definicji oblicz pochodną funkcji:
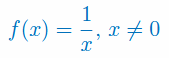
Korzystając z definicji wyprowadź wzór na pochodną ilorazu funkcji:
\(\left(\frac{f(x)}{g(x)}\right )'=\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}\)
Korzystając z definicji oblicz pochodną funkcji:
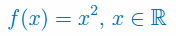
Korzystając z definicji zbadaj istnienie pochodnej funkcji \(f(x)=|x|\) w punkcie \(x_0=0\).
Korzystając z definicji oblicz pochodną funkcji logarytmicznej:
\(f(x)=\log_a(x),\,a>0,\,a\neq 1,\,x>0\)
Korzystając z definicji (\(h\to 0\)) oblicz pochodną funkcji potęgowej:
\(f(x)=x^n,\,\,n\in\mathbb{N}\)
Korzystając z definicji oblicz pochodną funkcji sinus:
\(f(x)=\sin(x)\)
Korzystając z definicji oblicz pochodną funkcji cosinus:
\(f(x)=\cos(x)\)
Korzystając z definicji oblicz pochodną funkcji sinus:
\(f(x)=\sin(x)+x^2-2x\)
Korzystając z definicji oblicz pochodną funkcji wykładniczej:
\(f(x)=a^x,\,\,a>0\)
Podaj wzór na pochodną funkcji
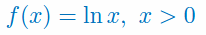
Podaj wzór na pochodną funkcji logarytmicznej
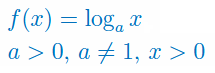
Podaj wzór na pochodną funkcji
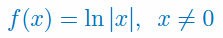
Podaj wzór na pochodną funkcji kwadratowej
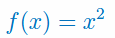
Podaj wzór na pochodną funkcji potęgowej
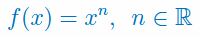
Podaj wzór na pochodną funkcji eksponencjalnej
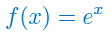
Podaj wzór na pochodną funkcji wykładniczej
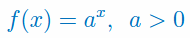
Oblicz pochodną funkcji
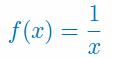
Oblicz pochodną funkcji
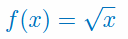
Podaj wzór na pochodną funkcji stałej
![]()
Oblicz pochodną funkcji

Podaj wzór na pochodną funkcji liniowej

Oblicz pochodną funkcji
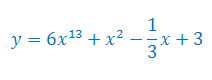
Oblicz pochodną funkcji
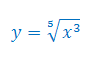
Oblicz pochodną funkcji
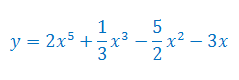
Oblicz pochodną funkcji
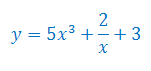
Oblicz pochodną funkcji
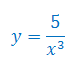
Oblicz pochodną funkcji

Oblicz pochodną funkcji
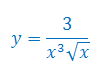
Oblicz pochodną funkcji
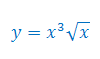
Oblicz pochodną funkcji
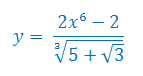
Oblicz pochodną funkcji

Oblicz pochodną funkcji
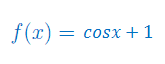
Oblicz pochodną funkcji
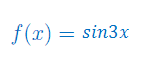
Oblicz pochodną funkcji
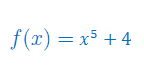
Oblicz pochodną funkcji
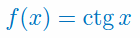
Oblicz pochodną funkcji
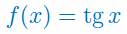
Podaj wzór na pochodną funkcji

Podaj wzór na pochodną funkcji
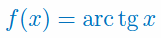
Podaj wzór na pochodną funkcji
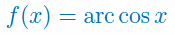
Podaj wzór na pochodną funkcji
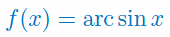
Podaj wzór na pochodną funkcji
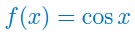
Podaj wzór na pochodną funkcji
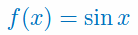
Oblicz pochodną funkcji
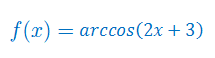
Jesteś w kategorii Pochodne funkcji zadania z rozwiązaniami
Pochodne funkcji stanowią jeden z najważniejszych działów Matematyki (a już napewno Analizy matematycznej) oraz są wykorzystywane w wielu innych dziadzinach - od fizyki po finanse. W tej kategorii znajdziesz setki zadań z rozwiązaniami z pochodnych funkcji, w tym zadania dotyczące liczenia pochodnej z definicji (za pomocą granic funkcji), obliczania pochodnych iloczynów i ilorazów funkcji oraz funkcji złożonych, a także przykłady pokazujące zastosowania pochodnych i liczenie pochodnych wyższych rzędów.
Liczenie pochodnych funkcji to inaczej różniczkowanie funkcji. Podstawową metodą liczenia pochodnych w danym punkcie jest wykorzystanie definicji a właściwie wzoru - liczymy po prostu granicę z ilorazu różnicowego funkcji. Inne metody liczenia pochodnych również polegają na zastosowaniu gotowych wzorów - na pochodną funkcji potęgowej, wykładniczej, logarytmicznej, funkcji trygonometrycznych oraz wzorów na pochodną iloczynu i ilorazu funkcji a także na pochodną funkcji złożonej. Chcąc obliczyć pochodne wyższego rzędu należy po prostu obliczyć pochodną kilka razy (w zależności od rzędu pochodnej), np. w przypadku pochodnej 2-go rzędu liczymy pochodną dwa razy - raz z wyjściowej funkcji i jeszcze raz "pochodną z pochodnej".
Warto próbować samodzielnie rozwiązać jak największą liczbę zadań z pochodnych funkcji i zaglądać do rozwiązań zamieszczonych na stronie jedynie w ramach podpowiedzi lub w celu sprawdzenia wyniku. Pod każdym zadaniem istnieje możliwość zadania pytania w komentarzu, warto z tej opcji korzystać, ponieważ tylko pełne zrozumienie rozwiązania zadania (oraz schematów i pojęć, które zostały w nim użyte) pozwala później na samodzielne rozwiązanie podobnego zadania w czasie trwania kolokwium lub egzaminu. Zadania z pochodnych są dość różnorodne, jednak po rozwiązaniu kilkudziesięciu przykładów zobaczysz, że schematy zaczynają się powtarzać, a różniczkowanie nie jest wcale takie trudne (w przeciwieństwie do całkowania funkcji, które jest dużo bardziej skomplikowane). Trzeba oczywiście opanować wszystkie podstawowe wzory na pochodne i wtedy mamy gwarancję, że żadna pochodna nie sprawi nam problemów.