Start Oblicz pochodną funkcji złożonej
\(y=x^{\sin x}\)
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Kategorie zadań z rozwiązaniami z matematyki wyższej
Strona 3 z 3
Pochodna funkcji - zadania z rozwiązaniami
Oblicz pochodną funkcji złożonej
\(y=(f(x))^{g(x)}\)
Oblicz pochodną funkcji złożonej
\(y={(\sin(x))}^{\cos(x)}\)
Oblicz pochodną funkcji złożonej
\(y={(\ln(x))}^{\cos(x)}\)
Napisz równanie stycznej do wykresu funkcji \(f(x)\) w punkcie \(x_0\)
Zbadaj monotoniczność i wyznacz ekstrema lokalne funkcji
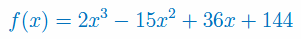
Zbadaj monotoniczność i wyznacz ekstrema lokalne funkcji
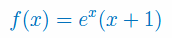
Kula wystrzelona z armaty zakreśla w powietrzu łuk opisany równaniem \(y=x-x^2\). Jaką maksymalną wysokość osiągnie kula?
Napisz równanie stycznej do wykresu funkcji \(f(x)\) w punkcie \(x_0\)
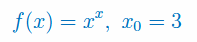
Zbadaj monotoniczność i wyznacz ekstrema lokalne funkcji
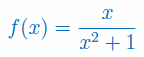
Zbadaj monotoniczność i wyznacz ekstrema lokalne funkcji
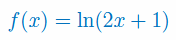
Zbadaj monotoniczność i wyznacz ekstrema lokalne funkcji
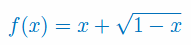
Oblicz drugą pochodną funkcji:
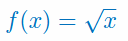
Oblicz trzecią pochodną funkcji:
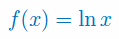
Oblicz pochodne \(f',\,f'',\,f'''\) dla funkcji:
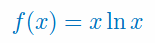
Wiedząc, że funkcja f ma trzy pierwsze pochodne, oblicz pochodne \(y',\,y'',\,y'''\) dla funkcji:
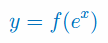
Znajdź wszystkie rozwiązania równania:
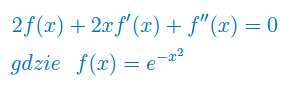
Oblicz pochodne rzędu 1,2,3,4 i 5 dla funkcji:
\(f(x)=\frac{1}{x}\)
Następnie podaj ogólny wzór na pochodną n-tego rzędu (\(n\in\mathbb{N}\)).
Oblicz pochodne rzędu 1,2,3,4 i 5 dla funkcji:
\(f(x)=\sin x\)
Następnie podaj ogólny wzór na pochodną n-tego rzędu (\(n\in\mathbb{N}\)).
Oblicz pochodne rzędu 1,2,3,4 i 5 dla funkcji:
\(f(x)=\cos x\)
Następnie podaj ogólny wzór na pochodną n-tego rzędu (\(n\in\mathbb{N}\)).
Oblicz pochodne rzędu 1,2,3,4 i 5 dla funkcji:
\(f(x)=2^x\)
Następnie podaj ogólny wzór na pochodną n-tego rzędu (\(n\in\mathbb{N}\)).
Oblicz n-tą pochodną wielomianu stopnia n (\(n\in\mathbb{N},\,\,a_1,a_2,...,a_n\in\mathbb{R}\)):
\(W(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\)
Ile wynosi pochodna rzędu \(n+k\), gdzie \(k=1,2,3,...\).
Strona 3 z 3
Jesteś w kategorii Pochodne funkcji zadania z rozwiązaniami
Pochodne funkcji stanowią jeden z najważniejszych działów Matematyki (a już napewno Analizy matematycznej) oraz są wykorzystywane w wielu innych dziadzinach - od fizyki po finanse. W tej kategorii znajdziesz setki zadań z rozwiązaniami z pochodnych funkcji, w tym zadania dotyczące liczenia pochodnej z definicji (za pomocą granic funkcji), obliczania pochodnych iloczynów i ilorazów funkcji oraz funkcji złożonych, a także przykłady pokazujące zastosowania pochodnych i liczenie pochodnych wyższych rzędów.
Liczenie pochodnych funkcji to inaczej różniczkowanie funkcji. Podstawową metodą liczenia pochodnych w danym punkcie jest wykorzystanie definicji a właściwie wzoru - liczymy po prostu granicę z ilorazu różnicowego funkcji. Inne metody liczenia pochodnych również polegają na zastosowaniu gotowych wzorów - na pochodną funkcji potęgowej, wykładniczej, logarytmicznej, funkcji trygonometrycznych oraz wzorów na pochodną iloczynu i ilorazu funkcji a także na pochodną funkcji złożonej. Chcąc obliczyć pochodne wyższego rzędu należy po prostu obliczyć pochodną kilka razy (w zależności od rzędu pochodnej), np. w przypadku pochodnej 2-go rzędu liczymy pochodną dwa razy - raz z wyjściowej funkcji i jeszcze raz "pochodną z pochodnej".
Warto próbować samodzielnie rozwiązać jak największą liczbę zadań z pochodnych funkcji i zaglądać do rozwiązań zamieszczonych na stronie jedynie w ramach podpowiedzi lub w celu sprawdzenia wyniku. Pod każdym zadaniem istnieje możliwość zadania pytania w komentarzu, warto z tej opcji korzystać, ponieważ tylko pełne zrozumienie rozwiązania zadania (oraz schematów i pojęć, które zostały w nim użyte) pozwala później na samodzielne rozwiązanie podobnego zadania w czasie trwania kolokwium lub egzaminu. Zadania z pochodnych są dość różnorodne, jednak po rozwiązaniu kilkudziesięciu przykładów zobaczysz, że schematy zaczynają się powtarzać, a różniczkowanie nie jest wcale takie trudne (w przeciwieństwie do całkowania funkcji, które jest dużo bardziej skomplikowane). Trzeba oczywiście opanować wszystkie podstawowe wzory na pochodne i wtedy mamy gwarancję, że żadna pochodna nie sprawi nam problemów.