Zbadać monotoniczność i wyznaczyć ekstrema lokalne funkcji
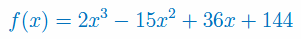
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Zbadać monotoniczność i wyznaczyć ekstrema lokalne funkcji
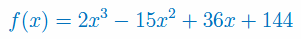
Zbadać monotoniczność i wyznaczyć ekstrema lokalne funkcji
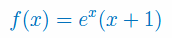
Zbadaj monotoniczność i wyznacz ekstrema lokalne funkcji
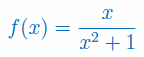
Zbadaj monotoniczność i wyznacz ekstrema lokalne funkcji
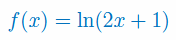
Zbadaj monotoniczność i wyznacz ekstrema lokalne funkcji
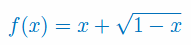
Zbadaj monotoniczność i wypukłość, wyznacz ekstrema i punkty przegięcia funkcji
\(f(x)=\frac{2\ln x}{x}\)
Jesteś w kategorii Monotoniczność, wypukłość i ekstrema funkcji zadania z rozwiązaniami krok po kroku
Funkcja jest monotoniczna, gdy jest rosnąca, malejąca lub stała. Jak sprawdzić monotoniczność funkcji? Można wykazać, że dla każdych dwóch argumentów (gdzie jeden jest mniejszy od drugiego) wartości funkcji im odpowiadające są w relacji: mniejszy - funkcja jest rosnąca, większy - funkcja jest malejąca, równy - funkcja jest stała. Do badania monotoniczności można użyć również pochodnej funkcji. Funkcja jest rosnąca na pewnym przedziale, gdy jej pochodna jest większa od zera dla argumentów należących do tego przedziału i malejąca, gdy jej pochodna jest mniejsza od zera na tym przedziale.
Ekstrema lokalne funkcji to minimum lub maksimum. Na wykresie ekstremum widoczne jest jako góra (maksimum lokalne) lub dolina (minimum lokalne). Aby wyznaczyć ekstrema lokalne funkcji należy obliczyć pochodną funkcji i znaleźć jej miejsca zerowe - są to potencjalne punkty w których mogą wystąpić ekstrema lokalne. Aby ustalić, czy jest to maksimum czy minimum lokalne należy sprawdzić monotoniczność funkcji z lewej i prawej strony tego punktu (można sprawdzić znak pochodnej). Gdy funkcja jest malejąca z lewej i rosnąca z prawej mamy minimum lokalne, w przeciwnym przypadku występuje maksimum lokalne.
Aby ustalić, czy funkcja jest wklęsła lub wypukła należy obliczyć drugą pochodną funkcji. Gdy druga pochodna jest większa od zera na pewnym zbiorze argumentów, to funkcja jest wypukła na tym zbiorze, natomiast gdy druga pochodna jest mniejsza od zera, to funkcja jest wklęsła. Punkt przegięcia funkcji to punkt (argument), w którym funkcja zmienia się z wypukłej na wklęsłą lub odwrotnie.