Start Niech \(n\in\mathbb{R}\). Oblicz granicę funkcji:
\(\lim\limits_{x\to 0} \frac{\sin(n\cdot x)}{\sin(x)}\)
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Kategorie zadań z rozwiązaniami z matematyki wyższej
Funkcje - zadania z rozwiązaniami
Oblicz granicę funkcji:
\(\lim\limits_{x\to 0} \frac{\sin(2x)}{\sin(x)}\)
Wykaż, że
\(\lim\limits_{x\to 0} \frac{tg x}{x}=1\)
Oblicz granicę funkcji
Korzystając z twierdzenia o dwóch funkcjach uzasadnić, że
\(\lim\limits_{x\to 0^+}\frac{\ln x}{x}=-\infty\)
Oblicz granicę funkcji stosując regułę de L'Hospitala
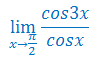
Oblicz granicę funkcji
\(\lim\limits_{x\to +\infty} \frac{\sqrt{x+1}-\sqrt{x}}{x}\)
Oblicz granicę funkcji
\(\lim\limits_{x\to \infty} \frac{\ln (x)}{\sqrt{x}}\)
Oblicz granicę funkcji
\(\lim\limits_{x\to \infty} \frac{\ln (x^2)}{\ln(x)}\)
Oblicz granicę funkcji
\(\lim\limits_{x\to \infty} \frac{\ln (2x)}{\ln(x)}\)
Oblicz granicę funkcji
\(\lim\limits_{x\to +\infty} \sqrt{x(x-\sqrt{x^2-1})}\)
Oblicz granicę funkcji
\(\lim\limits_{x\to +\infty} \left(\sqrt{x+1}-\sqrt{x}\right)\)
Oblicz granicę funkcji
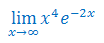
Oblicz granicę funkcji
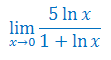
Oblicz granicę funkcji
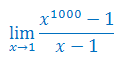
Oblicz granicę funkcji
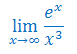
Oblicz granicę funkcji
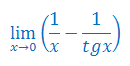
Oblicz granicę funkcji
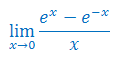
Oblicz granicę funkcji
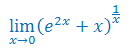
Oblicz granicę funkcji
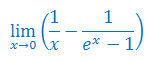
Oblicz granicę funkcji
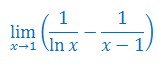
Oblicz granicę funkcji
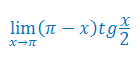
Obliczyć granicę funkcji
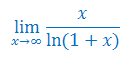
Obliczyć granicę funkcji
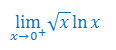
Obliczyć granicę funkcji
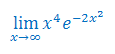
Obliczyć granicę funkcji
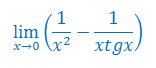
Oblicz granicę funkcji
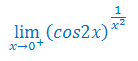
Oblicz granicę funkcji
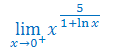
Oblicz granicę funkcji
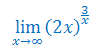
Oblicz granicę funkcji
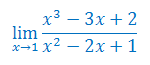
Korzystając z granic podstawowych wyrażeń nieoznaczonych oblicz granicę funkcji
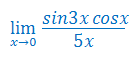
Korzystając z granic podstawowych wyrażeń nieoznaczonych oblicz granicę
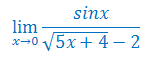
Obliczyć granicę niewłaściwą
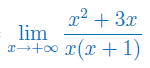
Obliczyć granicę niewłaściwą
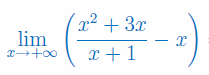
Oblicz granicę jednostronną funkcji
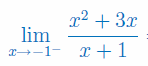
Oblicz granicę jednostronną funkcji
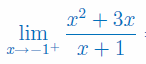
Korzystając z twierdzenia o trzech funkcjach oblicz granicę
Korzystając z twierdzenia o trzech funkcjach obliczyć granicę
\(\lim\limits_{x\to \infty}\frac{\sin x}{x^4+1}\)
Oblicz granicę funkcji
\(\lim\limits_{x\to 1} \frac{x^2-1}{x-1}\)
Oblicz granicę funkcji
\(\lim\limits_{x\to 1} \left(\frac{x}{x-1}-\frac{1}{\ln x}\right)\)
Oblicz granicę funkcji
\(\lim\limits_{x\to +\infty} \left(x-\ln x\right)\)
Oblicz granicę funkcji
\(\lim\limits_{x\to 0^+} x^x\)
Korzystając z twierdzenia o trzech funkcjach wykaż, że:
\(\lim\limits_{x\to 0}x\sin \left(\frac{1}{x}\right)=0\)
Udowodnić, że przy \(x\to a\) i \(x\to b\) (\(a\neq b\), \(a,b\in\mathbb{R}\)) nie istnieje granica funkcji
\(f(x)=\frac{1}{(x-a)(x-b)}\)
Oblicz granicę funkcji
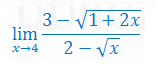
Oblicz granicę jednostronną funkcji
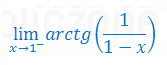
Oblicz granicę jednostronną funkcji
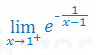
Udowodnić, że granica funkcji nie istnieje
Oblicz granicę wielomianu:
\(W(x)=3x^3-2x^2+5x-7\)
w \(-\infty\) i \(+\infty\).
Oblicz granicę wielomianu:
\(W(x)=-2x^4+x^3+5x^2-8x\)
dla \(x\to -\infty\) i \(x\to +\infty\).
Jesteś w kategorii Funkcje zadania z rozwiązaniami
W tym dziele znajdziesz kilkadziesiąt zadań z rozwiązaniami krok po kroku z zakresu funkcji jednej zmiennej. Zobacz przykłady określania dziedziny i własności funkcji, obliczania granic, sprawdzania ciągłości funkcji, wyznaczania asymptot oraz sprawdzania monotoniczności i ekstremów. Ucząc się funkcji na przykładach poznasz typowe schematy rozwiązywania zadań, np. jak poradzić sobie z symbolami nieoznaczonymi przy obliczaniu granic funkcji (reguła de L'Hospitala), jak liczyć asymptoty funkcji i wiele innych. Pod większością zadań znajdziesz wyjaśnienie najważniejszych metod, schematów, pojęć i wzorów.
Zachęcam do próby samodzielnego rozwiązywania zadań z funkcji i sięganie do rozwiązań na stronie w ramach podpowiedzi lub w celu sprawdzenia wyniku. Jeśli czegoś nie rozumiesz zapytaj w komentarzu pod zadaniem - kto pyta nie błądzi i lepiej wyjaśnić wszystkie wątpliwości tak aby samemu potrafić rozwiązać podobne zadania. Na koiniec pozostaje mi jedynie życzyć Ci powodzenia w nauce i świetnych wyników na egzaminie!