Start Podaj rozkład funkcji wymiernej na rzeczywiste ułamki proste (nie obliczaj współczynników)
\(\frac{2x^4-x^3+1}{x(x-4)^3(x^2+1)}\)
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Kategorie zadań z rozwiązaniami z matematyki wyższej
- Pochodne funkcji (122)
- Całki (215)
- Całki nieoznaczone (121)
- Całki oznaczone (32)
- Całki niewłaściwe (24)
- Całki podwójne (16)
- Całki potrójne (8)
- Całki krzywoliniowe (14)
- Funkcje (145)
- Szeregi i ciągi liczbowe (115)
- Ciągi liczbowe (20)
- Granice ciągów (38)
- Szeregi liczbowe (36)
- Szeregi potęgowe i funkcyjne (17)
- Szeregi Fouriera (4)
- Równania różniczkowe (44)
- Macierze i wyznaczniki (90)
- Działania na macierzach (22)
- Wyznacznik macierzy (24)
- Macierz odwrotna (16)
- Równania macierzowe (14)
- Rząd macierzy (10)
- Wartości i wektory własne (4)
- Liczby zespolone (134)
- Wielomiany (37)
- Równania i nierówności (3)
- Układy równań liniowych (29)
- Geometria analityczna (34)
- Logika (44)
- Zdania logiczne (22)
- Działania na zbiorach (22)
- Rachunek prawdopodobieństwa (84)
- Kombinatoryka (36)
- Prawdopodobieństwo (38)
- Zmienna losowa (6)
- Funkcja charakterystyczna (4)
- Statystyka matematyczna (5)
- Finanse (6)
Podaj rozkład zespolonej funkcji wymiernej na zespolone ułamki proste (nie obliczaj współczynników)
\(\frac{2iz}{(z-2)^3(z^2+1)}\)
Rozwiąż równanie:
\(x^4+2x^2-3=0,\,\,x\in\mathbb{R}\)
Rozwiąż równanie:
\(9^x-6^x=4^x,\,\,x\in\mathbb{R}\)
Rozwiąż równanie:
\(x^4-1=0,\,\,x\in\mathbb{R}\)
Rozwiąż układ Cramera z 2 niewiadomymi:
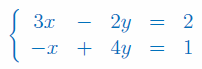
Rozwiąż układ równań liniowych z 2 niewiadomymi:
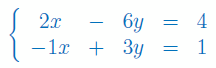
Rozwiąż układ Cramera z 3 niewiadomymi:
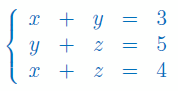
Stosując wzory Cramera wyznacz niewiadomą y
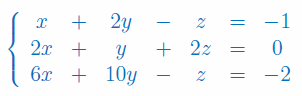
Zbadać dla jakich wartości parametru p układ równań jest układem Cramera. Następnnie wyznaczyć wartości niewiadomych
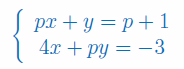
Rozwiązać układ równań metodą wyznacznikową:
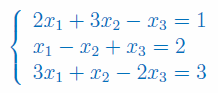
Inwestor chce kupić akcje za 100 tys. zł, chcąc uzyskać przeciętny (średni) zysk w ciagu pół roku na poziomie 13,5%, przy ryzyku w wysokości 10%. Doradca inwestycyjny oferuje mu 3 pakiety akcji o róznym średnim wzroście i ryzyku:
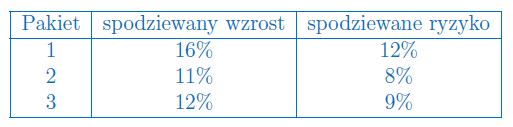
Jakie kwoty pieniędzy powinien zainwestować inwestor w akcjie z każdego pakietu, żeby zrealizować swój cel inwestycyjny?
Zbadaj liczbę rozwiązań układu równań w zależności od parametru p. Dla p=2, korzystając ze wzorów Cramera wyznacz wartość niewiadomej y:
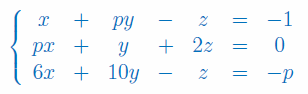
Rozwiąż układ równań z 2 niewiadomymi (x,y) metodą przeciwnych współczynników oraz za pomocą wzorów Cramera:
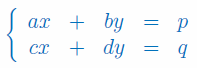
gdzie \(a,b,c,d,p,q\in\mathbb{R}\).
Dla jakich wartości parametru p układ równań jest układem Cramera:
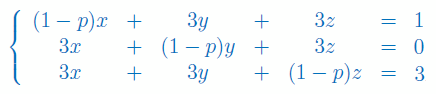
Rozwiąż układ równań stosując wzory Cramera
\(\left\{\begin{array}{ccccccccccc}x_1&+&x_2&+&x_3&+&x_4&+&x_5&=&5\\2x_1&+&x_2&-&x_3&+&3x_4&+&x_5&=&6\\5x_1&-&2x_2&+&x_3&+&x_4&-&x_5&=&4\\-x_1&+&x_2&+&3x_3&+&2x_4&+&2x_5&=&7\\x_1&-&x_2&+&x_3&-&x_4&+&x_5&=&1\end{array}\right.\)
Rozwiąż układ równań stosując wzory Cramera
\(\left\{\begin{array}{ccccccccc}x_1&+&x_2&+&x_3&+&x_4&=&4\\2x_1&+&x_2&-&x_3&+&3x_4&=&5\\5x_1&-&2x_2&+&x_3&+&x_4&=&5\\-x_1&+&x_2&+&3x_3&+&2x_4&=&5\end{array}\right.\)
Rozwiąż układ równań stosując wzory Cramera
\(\left\{\begin{array}{ccccccc}x&+&y&+&z&=&5\\2x&+&2y&+&z&=&3\\3x&+&2y&+&z&=&1\end{array}\right.\)
Rozwiąż układ równań metodą eliminacji Gaussa:
\(\left\{\begin{array}{ccccccc}x&+&2y&+&3z&=&4\\&& y& +&2z&=&3\\&&&&4z&=&4\end{array}\right.\)
Rozwiązać układ równań metodą eliminacji Gaussa:
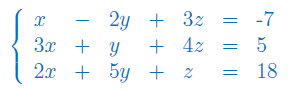
Rozwiązać układ równań przy użyciu metody eliminacji Gaussa:
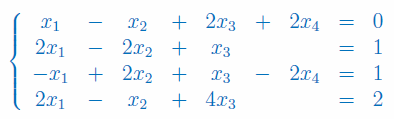
Rozwiąż metodą eliminacji Gaussa:
\(\left\{\begin{array}{ccccccccc}2x_1&+&x_2&-&x_3&+&x_4&=&1\\&& x_2& +&3x_3&-&3x_4&=&1\\x_1&+&x_2&+&x_3&-&x_4&=&1\end{array}\right.\)
Rozwiąż układ metodą eliminacji Gaussa:
\(\left\{\begin{array}{ccccccccc}2x_1&+&x_2&-&x_3&+&x_4&=&1\\3x_1&-&2x_2&+&2x_3&-&3x_4&=&2\\5x_1&+&x_2&-&x_3&+&2x_4&=&-1\\2x_1&-&x_2&+&x_3&-&3x_4&=&4\end{array}\right.\)
Rozwiąż układ metodą eliminacji Gaussa:
\(\left\{\begin{array}{ccccccc}2x_1&+&x_2&+&x_3&=&1\\3x_1&-&x_2&+&3x_3&=&2\\x_1&+&x_2&+&x_3&=&0\\x_1&-&x_2&+&x_3&=&1\end{array}\right.\)
Zbadaj liczbę rozwiązań układu równań w zależności od parametru p:
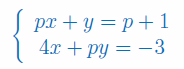
Zbadaj liczbę rozwiązań układu równań w zależności od parametru p:
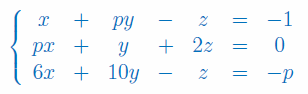
Dla jakich wartości parametru p układ równań ma tylko jedno rowiązanie:
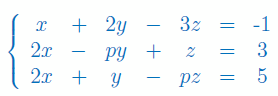
Stosując twierdzenie Kroneckera-Capellego zbadaj liczbę rozwiązań układu równań liniowych. Następnie rozwiąż układ (jeśli to konieczne przedstaw rozwiązania za pomocą parametrów):
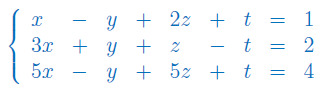
Określić liczbę rozwiązań układu równań przy użyciu twierdzenia Kroneckera-Capellego:
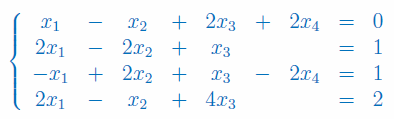
Zapisz macierz główną układu równań:
\(\left\{\begin{array}{ccccccc}x&-&4y&+&5z&=&2\\&& 2y& -&z&=&1\\4x&+& 2y&+&z&=&0\end{array}\right.\)
Podać przykład sprzecznego układu równań liniowych
Zapisz układ równań w postaci macierzowej:
\(\left\{\begin{array}{cccccccccc}2x&+&y&-&z&+&3t&=&1\\-x&+&7y&-&3z&-&5t&=&2\\2x&&&+&9z&-&2t&=&3\\x&+&y&&&+&2t&=&4\end{array}\right.\)
Rozwiązując odpowiedni układ równań, wyznacz równanie trójmianu kwadratowego przechodzącego przez punkty:
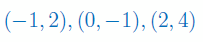
Rozwiąż układ równań z 3 niewiadomymi metodą macierzową:
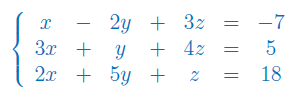
Oblicz iloczyn skalarny wektorów
\(\overline{u}=[1,-3,2\sqrt{2}],\,\,\overline{v}=\left[0,1,-\frac{1}{2}\right]\)
Oblicz iloczyn skalarny wektorów i sprawdź czy są one prostopadłe
\(\vec{a}=[1,0,-3],\,\,\vec{b}=\left[3,10,1\right]\)
Zbadaj prostopadłość wektorów:
\(\vec{a}=[-3,2,7],\,\,\vec{b}=\left[4,-1,2\right]\)
Oblicz kąt między wektorami
\(\overline{u}=[-2,1,2],\,\,\overline{v}=\left[0,1,1\right]\)
Oblicz iloczyn wektorowy wektorów
\(\vec{u}=[-1,3,2],\,\,\vec{v}=\left[-1,2,-5\right]\)
Sprawdź, czy wektory są równoległe
\(\vec{u}=[1,2,3],\,\,\vec{v}=\left[2,4,6\right]\)
Oblicz pole równoległoboku rozpiętego na wektorach
\(\vec{a}=[1,2,3],\,\,\vec{b}=\left[3,2,-1\right]\)
Wiedząc, że \(\vec{a}\circ \vec{b}=3\) oraz \(|\vec{a}|=1,\,\,|\vec{b}|=2\) oblicz iloczyn skalarny wektorów \(\vec{p}\circ \vec{q}\), gdzie
\(\vec{p}=\vec{a}+\vec{b},\,\,\vec{q}=2\vec{a}-5\vec{b}\)
Dla jakich parametrów \(a,b\in\mathbb{R}\), wektory \(\vec{u}\) i \(\vec{v}\) są prostopadłe:
\(\vec{u}=[a+b,1,b],\,\,\vec{v}=\left[-1,2a,3\right]\)
Wyznacz wektor prostopadły do wektorów:
\(\vec{u}=[-1,3,2],\,\,\vec{v}=\left[-1,2,-5\right]\)
Wyznacz wektor równoległy do płaszczyzny zawierającej wektory:
\(\vec{u}=[4,-1,5],\,\,\vec{v}=\left[3,1,-7\right]\)
Oblicz iloczyn skalarny wektorów:
\(\vec{u}=\vec{i}-\vec{j}+\vec{k},\,\,\vec{v}=5\vec{i}-3\vec{k}\)
Napisać równanie parametryczne prostej przechodzącej przez punkt \(P=(-1,2,0)\) i równoległej do wektora
\(\overline{u}=[1,2,3]\)
Napisać równanie ogólne płaszczyzny przechodzącej przez punkt \(P=(2,1,-3)\) i prostopadłej do wektora
\(\vec{n}=[-1,7,4]\)
Napisać równanie parametryczne płaszczyzny przechodzącej przez punkt \(P=(-1,2,-4)\) i równoległej do wektorów
\(\vec{a}=[1,0,-2],\,\,\,\vec{b}=[0,-8,-5]\)
Przekształć prostą \(l\) daną w postaci kierunkowej
\(\frac{x}{-4}=\frac{y+1}{2}=\frac{z+2}{7}\)
na postać parametryczną i krawędziową.
Na tej stronie znajdziesz około tysiąca zadań z rozwiązaniami i przykładów krok po kroku głównie z zakresu matematyki wyższej, jak również z matematyki na poziomie liceum. Zadania podzielone są na działy tematyczne zazwyczaj według przedmiotów i tematów wymaganych na studiach, np. zadania z pochodnych funkcji i całek (analiza matematyczna), macierzy i liczb zespolonych (algebra liniowa), zmiennych losowych i prawdopodobieństwa (rachunek prawdopodobieństwa) itd.
W każdej kategorii znajdziesz zadania o różnym poziomie trudności, a pod każdym zadaniem znajdziesz wiele wskazówek jak przebiega rozwiązanie, potrzebne definicje i wzory oraz podsumowanie schematów użytych w rozwiązaniu. Często rozwiązanie zadania omówione jest wręcz krok po kroku. Warto starać się samodzielnie rozwiązać jak najwięcej zadań znajdujących się na stronie, ponieważ są tu zebrane typowe zadania z kolokwiów i egzaminów z polskich uczelni. Nauka matematyki na przykładach i konkretnych zadaniach jest najbardziej efektywna - potwierdzają to badania naukowe. Trzeba tylko uczyć się (a właściwie analizować przykłady i rozwiązywać zadania) konsekwentnie i wytrwale, a efekty w postaci lepszego zrozumienia pojęć i schematów oraz umiejętność samodzielnego rozweiązywania podobnych zadań przyjdą same.
Pamiętaj, że zawsze masz możliwość zadania pytania w komentarzu pod każdym zadaniem - warto z tej możliwości korzystać, ponieważ na tej stronie nie ma głupich pytań i każde, nawet najgłupsze pytanie znajdzie swoją odpowiedź. Powodzenia w zrozumieniu matematyki!